Calcul du centre de gravité d'un pentagone irrégulier

[invitef98b63f8]

Bonjour, je suis en train de faire un DM de mathématiques dont voici le sujet (pour le contexte)

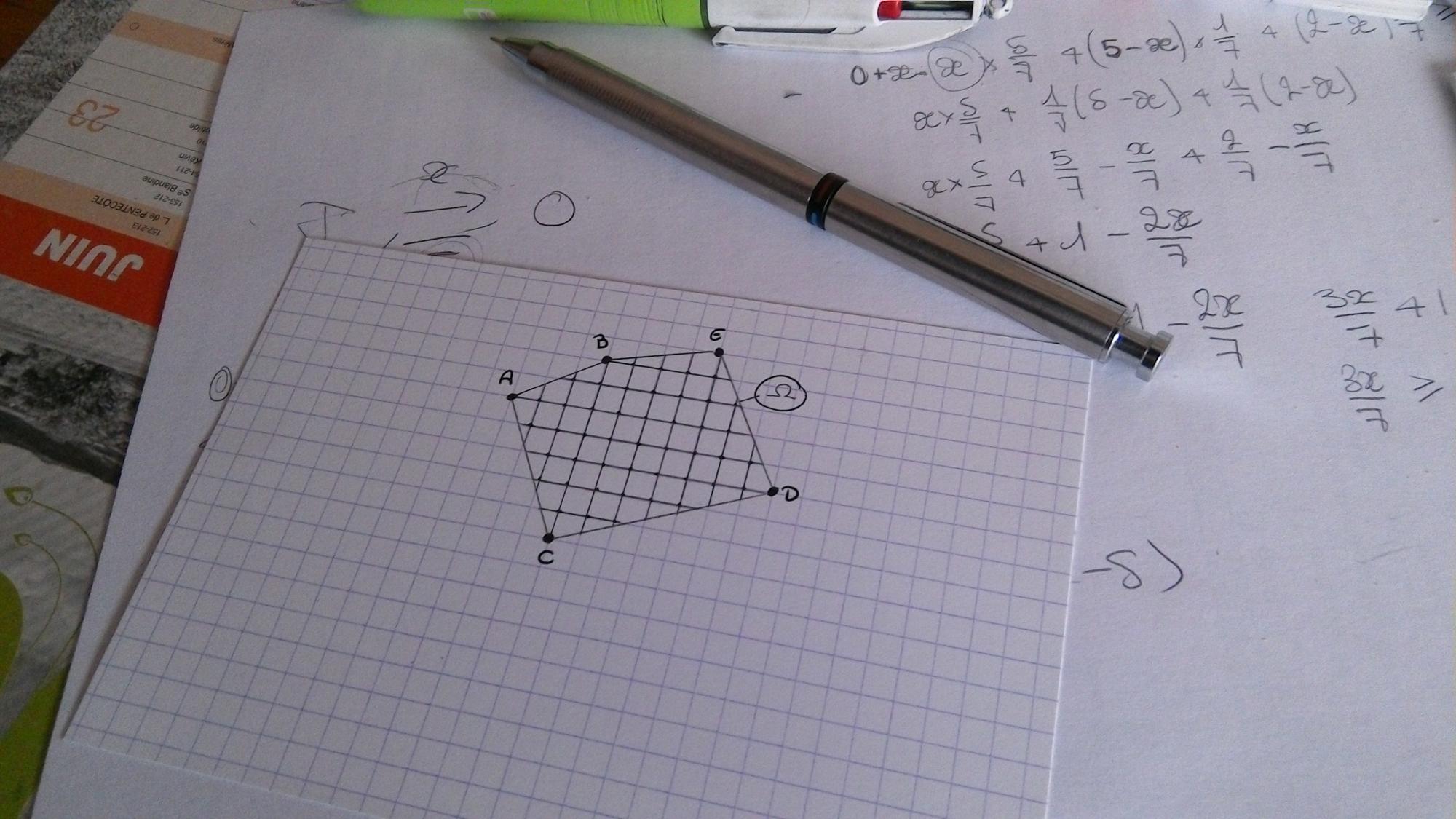
Le réseau des rues de New-York peut être modélisé par un quadrillage orthonormal. La distance entre deux points de cette ville est alors égale au nombre minimal de côtés de carreaux que l’on doit suivre pour relier les deux points. La situation de cinq centres universitaires est représentée par les points A , B , C , D et E ;on veut installer une bibliothèque telle que la somme des distances aux cinq centres soit la plus petite possible. Où doit-on placer la bibliothèque ?

Je cherche à déterminer le centre de gravité de la figure pour avoir une idée de l'endroit où pourrait se trouver cette bibliothèque. La figure est un pentagone irrégulier et je n'ai pas les coordonées des points puisque aucun repère n'est tracé. Pourriez-vous m'aider ?
Merci d'avance pour vos réponses.
-----

[invite51d17075]

Bonjour, je suis en train de faire un DM de mathématiques dont voici le sujet (pour le contexte)
.

l'énoncé se résume à cela ?

[invite51d17075]

D'autant que dans un cas général, la position optimale n'est pas forcement celle qui est la plus proche du centre de gravité.
essaye avec 4 points alignés assez proches et un seul point plus éloigné et " en biais" / aux autres.

[invitef98b63f8]

Oui, c'est un des exercices du DM, y'a deux autres exercices.

[A voir en vidéo sur Futura]

[invite51d17075]

les centres et la bibliothèque sont bien aux intersections , ou pas forcement ?

[invitef98b63f8]

On dispose de ce schéma :
Pièce jointe 361863

Je ne comprends pas vraiment comme je suis censé procéder. Ils sont bien aux intersections du quadrillage.

[invite51d17075]

Ta pièce jointe n'est pas valide.
fais une photo que tu ajoutes ensuite en utilisant le bouton qui ressemble à un carré dans le menu au dessus du texte à envoyer.

[invite51d17075]

pour reprendre ma remarque plus haut.
pour simplifier je prend tous les points aux intersections et je compte 1 pour chaque bloc.
coords imaginées
A(0;0), B(0,1),C(0,2),D(0,3),E(3,5)
la centre de gravité le plus proche ( sur une intersection ) est en G(2,1)
la somme des distances ( au sens donné dans l'exercice ) de celui ci aux 4 points vaut 13.
Or, le point situé en (0,2) par exemple est lui à une distance ( somme ) qui vaut 10.

[invitef98b63f8]

Pardon, voici l'image :

[invitef98b63f8]

Je l'ai reproduite à l'identique et j'ai tracé les segments qui relient chaque point entre eux. Le petit Omega en haut, c'est parce que c'est un DM sur les probabilités (espérance mathématiques, écart-type etc...) Et je considère les points âge l'intérieur comme mon univers.

[gg0]

Bonjour Redister.

En attendant que ta pièce jointe soit lisible ("en attente de validation"), rien ne t'empêche de mathématiser le problème (sans chercher une réponse automatique non pensée, comme ton "centre de gravité") pour voir ce que tu dois faire. Si ta bibliothèque est à la position (x,y), quelle est la somme des distances ?

Cordialement

NB : le centre de gravité n'a jamais été une question de distance minimale.

[invite9dc7b526]

Le centre de gravité de n points minimise la somme des carrés des distances à ces points (théorème d'Huyghens) mais pas en général la somme des distances.

[invite51d17075]

On voit enfin ton croquis.
tu peux tout à fait exprimer les coords de tes points en prenant par exemple C en (0,0) ; D(8,3) ; etc.
et ta bibliothèque en (x,y)
tu peux facilement écrire la somme des distances de ta bibliothèque aux diff points en fonction de x et y

[invite51d17075]

D (7,3) pardon.

[invitef98b63f8]

On voit enfin ton croquis.
tu peux tout à fait exprimer les coords de tes points en prenant par exemple C en (0,0) ; D(8,3) ; etc.
et ta bibliothèque en (x,y)
tu peux facilement écrire la somme des distances de ta bibliothèque aux diff points en fonction de x et y

D'accord je suis bête oui, je vais faire ça. En fait, je pensais calculer les coordonnées du centre de gravité, avec un peu de chances, il sera au milieu d'un carreau et donc il y aura 4 points possibles correspondant à la position de la bibliothèque. J'ai remarqué qu'en comptant le nombre de côtés par lesquelles on passait pour atteindre un point, le chemin le plus rapide, peut importe la façon dont on le prennait, faisait toujours le même nombre de côtés.

[invite51d17075]

En fait tu voulais certainement parler de barycentre ( qu'il ne faut pas confondre ).
de mon coté, je n'ai pas vu qu'il s'agissait d'un exercice demandant à être approché sous l'angle des espérances mathématiques, etc....

[invitef98b63f8]

En faisait les calculs, c'est-à-dire la moyenne des abscisses des points et la moyenne des ordonnées, je trouve que le centre de gravité du pentagone est (1.6 ; 4.6) avec C(0 ; 0). Il est donc à peu près au milieu de la figure au centre d'un carreau. Mais comme l'a dit @minushabens, je crois pas que ça va m'aider. Si je continue mon raisonnement, j'ai quatres points qui peut correspondre à ma bibliothèque, et des dizaines de chemins possibles à partir de chaque point. Quelle est la différence entre un barycentre et un centre de gravité ? Parce que c'est la même chose d'après Google. Et un isobarycentre, c'est le centre géométrique de la figure ? Ne serait-ce pas plutôt que je devrais essayer de faire ?

[invitef98b63f8]

Justement, @ansset, notre professeur nous avait dit : "on dirait pas, mais y a des probabilités"... Alors où elles sont cachées ? Bonne question ... Mais je commence seulement à vraiment réfléchir à l'exercice donc...

[invitef98b63f8]

En faisant mes calculs de chemins, j'obtiens comme somme du nombre de côtés traversés en fonction des points possibles correspondant à le bibliothèque : 27,28,28,29. Bon j'ai vérifié il n'y a pas d'erreurs de calculs en principe.

[invite51d17075]

sans trop avoir réfléchi à ton pb globalement , j'ai une solution avec une somme de distance=26

[invite51d17075]

En plaçant la biblio en (0,5) soit en ligne directe avec les trois points C,B et A.

[invitef98b63f8]

sans trop avoir réfléchi à ton pb globalement , j'ai une solution avec une somme de distance=26

quelqu'un dans la classe avait aussi ce résultat, mais tu comptes à la main les côtés des carreaux par lesquels tu passes ou seulement en utilisant la formule qui permet de calculer la longueur d'un segment dans un repère ?

[invitef98b63f8]

Mais je ne comprends pas comment tu as trouvé les coordonnées de ce point ?

[invite51d17075]

non loin du barycentre et surtout qui propose un maximum d'alignements directs.
je n'ai pas cherché à modéliser tout cela par calcul ( par fainéantise ) , ce qu'il faudrait certainement faire !

[invite51d17075]

je vais regarder tout à l'heure pour une approche purement mathématique.
sinon, évite de confondre l'isobarycentre et le centre de gravité.
il ne sont confondus que pour tout triangle, ou dans le cas de figure à N cotés, pour des formes particulières ( avec les symétries nécessaires)

[invite51d17075]

ce n'est pas trivial pour un exercice de Lycée ( si on doit le résoudre purement mathématiquement )
est ce un exercice spécial ?
une approche un peu heuristique est elle admise dans le contexte.
voilà ce qu'on peut faire avec un début mathématique.
En supposant que l'on puisse se déplacer en ligne droite l'optimisation de la somme des distance donne comme résultat :
M(1,5) ( après un calcul/modèle un peu lourd ) pour le point le plus proche du point théorique.
celui ci offre une somme des distances ( le long des rues ) de 27
en cherchant un point proche le point M(0,5) fait gagner une longueur car
-on en gagne 1 ( à chaque fois ) pour les points A,B et C ( car on optimise le nb d'alignements directs )
-on en perd 1 pour les point D et E ; résultat 26

je n'ai pas mieux pour l'instant.
je suis sur qu'il doit y avoir un truc plus subtil à proposer.

[invitef98b63f8]

C'est un exercice de DM voilà, je pense qu'une approche "heuristique" est autorisé mais il faut néanmoins resté dans le programme de 1èreS. Avec mon père, nous avons tenté de faire quelques essais. Le problème se rapproche du problème classique du plus court chemin. Merci pour vos propositions de pistes de recherches.

[invite9dc7b526]

sinon, évite de confondre l'isobarycentre et le centre de gravité.

tiens, quelle est la différence? j'ai toujours pensé que c'était la même chose.

[invite51d17075]

Au temps pour moi ! désolé.

[jacknicklaus]

je suis sur qu'il doit y avoir un truc plus subtil à proposer.

Le lien avec les probabilités reste encore une énigme, du moins pour moi... y aurait il une grosse astuce ?