stucture algébrique
salut le monde j'éspere vous allez tous bien .
après avoir démontré l'unicité de l'élément neutre en utilisant la définition d'un élément neutre
cependant lors d'une séance sur les matrices on a pu trouvé deux éléments neutres la matrice I2 et une matrice B
et on a pu les démontrer mais comment ça l élément neutre est il pas unique ?
Dans un monoïde l'élément neutre s'il y en a un est toujours unique. Quelle est cette matrice B et de quel ensemble de matrices est-ce que tu parles? (quelle dimension, sur quel anneau, s'agit-il de toutes les matrices ou de celles ayant une certaine forme)
Et pour quelle opération aussi... l'élément neutre pour l'addition est différent de l'élément neutre pour la multiplication
SALUT merci d'avance
voila la matrice M2 , pour la multiplication *
M2(R ) tels que
M (X ) =
(x x )
(x x )
qui normalement pour élément neutre
( 1 0 )
( 0 1 )
pardon pour la mauvaise symbolisation et du même on trouve un autre élément neutre la matrice
( 1/2 1/2 )
(1/2 1/2 )
la matrice est formé de 2colonnes
Pourquoi dis-tu que ta deuxième matrice est un élément neutre pour le produit de matrice 2x2 ? C'est faux de façon évidente : il suffit de faire une multiplication par une matrice quelconque (à coefficients différents) pour le voir. Ne confonds-tu pas avec un produit défini sur des matrices 2x2 particulières (4 coefficients égaux), donc il s'agirait d'un groupe tout différent.
Cordialement.
c'est aussi ce que je comprends de sa notationEnvoyé par gg0
M (x ) =
(x x )
(x x )
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
x veut dire le variable x qui est réel pour l'opération multiplication *
c'est tout parce que j'ai pas pu ien shématisé la matrice
Donc finalement, il y a bien unicité, puisqu'il s'agit de deux groupes différents, et la preuve d'unicité est bien applicable, soit dans (M2(R),*) soit dans ({M(x)},*).
As-tu compris ?
j'ai pas compris pouvez vous m'expliquer
L'ensemble des matrices 2x2 dont les quatre coefficients sont égaux n'est pas un sous-ensemble - a fortiori pas un sous-groupe - de l'ensemble des matrices 2x2 inversibles. Tous les deux sont des sous-ensembles (disjoints) de l'ensemble des matrices 2x2. Chacun a son élément neutre et il n'y a pas de contradiction avec le fait que l'élément neutre est unique.
ben :
dans M2 l'élément neutre c'est
1/2 1/2
1/2 1/2
et non pas
1 0
0 1
puisque ce dernier n'appartient pas au groupe M2
Et dans M l'élément neutre est
1 0
0 1
et non pas
1/2 1/2
1/2 1/2
qui ne vérifie trivialement pas la condition de neutralité dans M
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
Si on considère maintenant l'ensemble A={matrices à coefficients égaux} U {Id}, donc l'ensemble précédent auquel on a adjoint la matrice identité. Cet ensemble est toujours stable pour la multiplication et son élément neutre est Id. La matrice "1/2" n'est plus élément neutre et hormis Id, les autres matrices n'ont plus d'inverse...
Parklee,
il serait bon que tu revoies la définition d'élément neutre, en relisant tous les mots.
Cordialement.
il me manquait que e appartient à l'ensemble M2 Oui c'est bien la matrice 1/2 ...
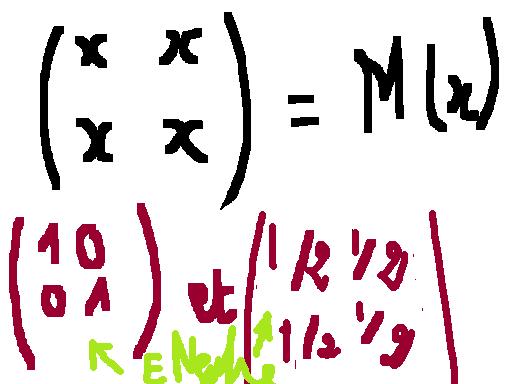
c est tout simplement relatif à la définition de l’élément neutre
Pas seulement.
Ta matrice "1/2" appartient bien à l'ensemble M des matrices 2x2, mais n'est pas un élément neutre pour la multiplication des matrices 2x2.
"Soit E un ensemble et T une loi de composition interne sur E; l'élément e de E est un élément neutre pour T si pour tout élément x de E, eTx=xTe=x".
En notant I la matrice unité de la multiplication des matrices 2x2 et J ta "matrice 1/2", alors :
Pour tout élément A de M2, AJ=JA=A
Pour tout élément A de M, AI=IA=A
Et, comme tu l'as vu, I n'est pas dans M2; réciproquement, J est bien dans M, mais AJ=JA=A n'est pas vrai "pour tout élément de M".
A noter : Si la matrice A est dans M2, AJ=A=AI, donc AJ-AI=0 (matrice nulle) et donc A(J-I)=0. On dit que les matrices de M2 (et aussi J-I) sont des diviseurs de 0. Un produit de matrice peut être nul sans qu'aucun des facteurs ne soit nul.
Cordialement.
Je trouve cet exemple intéressant. Si on voit M (je reprends les notations de gg0) comme une algèbre (unitaire) sur R, M2 est un sous-espace vectoriel de M, de dimension 1. Il est stable pour la multiplication, c'est donc une sous-algèbre de M. Elle est unitaire mais son élément unité n'est pas celui de M.
c 'est dur cette leçon en terminale j'ai la sensation que j suis en prépas
merciiii je comprends bien
