Si on part de théorème de pythagore vers fermat peut on trouver de simple solutions?

[jean reaver]

Pour montrer que a^2+b^2=c^2 existe on choisit
deux rectangle de côtés (a et b) ,on les disposent de façon
qu'ils forment une identité remarquable (a+b)^2.
Par la suite on découpe les deux rectangles et on
obtient ainsi : 4 triangles rectangles,dont les 4 diagonales
donnent un carré de côté c. On déduit que (a+b)^2-2ab=a^2+b^2=c^2 .
Il reste à définir quelles sont les valeurs qui peuvent satisfaire à ceci ?
D'abord il faut se baser sur la propriété de l'addition (associativité)
de sorte que les deux termes sont des carrés.Un connu et le second non.
(n+1)^2=n^2+(2*1*n+1^2)*
(n+1)^2=n^2+2n+1
Pour satisfaire au théorème ,il faut que (2n+1) soit aussi un carré.
2n+1=x^2
solution :
n=2*(m^2-m)
x=1-2*m
m appartient à Z.
ex: pour m=2
n=2*(2^2-2)=4
x=1-2^2=-3
m. n .x .x^2
2 .4 .-3 .9
Par conséquent
2n+1=x^2
2.4+1=9
et
(4+1)^2=4^2+(2.4+1)
25=16+9 .
De même ,pour continuer
Si n^2 et (n+1)^2 se succèdent alors
(n+1)^2-n^2=2n+1
Par ailleurs la somme de la suite 2n+1 donnent tous les carrés.
1+3+4+5+7+9+......2n-1
Si on trouve un carré dans cette series on s'arrête
(1+3+4+5+7)+9 on sait d'avance que la somme des termes qui précèdent est
un carré.
(1+3+5+7)+9
1 4 9 16 25
16+9=25 vrai
Dans ce même exemple ,Cherchons Pour La puissance 3?
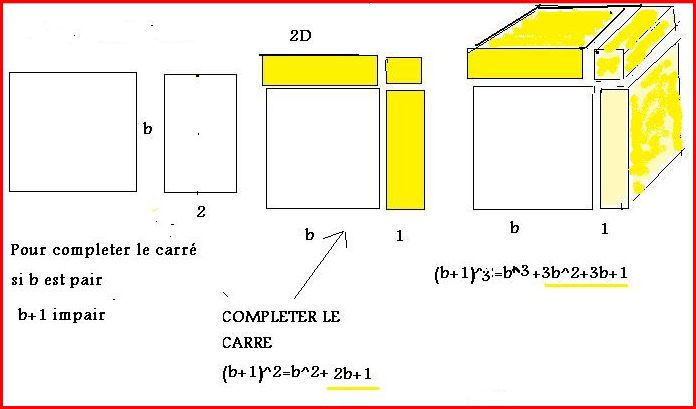
(1+n)^3=n^3+3 n^2+3 n+1
3 n^2+3 n+1=x^3
solution dans z
n=-1
x=1
3 (-1)^2+3 (-1)+1=1^3
3 +( -2) =1

Ceci confirme que l'addition de la series* ne contient aucun nbr cube.
SERIES* 1+7+19+37+61+91......3 n^2+3 n+1 (nombres héxagonaux)
SOMME 1 8 27 ............ n^3
a^3+b^3=c^3 n'a pas de solution

l'astuce revient au fait ,si on trouve un nbr V^n dans la series et qui corespond au même rang que U^n (somme)on déduit que le theoreme existe.
sinon on partage le nombre en deux moitiès le nombre.
00.01.02.03.04.05.06.07.08.(09 ).10.11.12
25.24.23.22.21.20.19.18.17.(16 ).15.14.13
-----

[eudea-panjclinne]

Dans ce même exemple ,Cherchons Pour La puissance 3?
(1+n)^3=n^3+3 n^2+3 n+1
3 n^2+3 n+1=x^3
solution dans z
n=-1
x=1
3 (-1)^2+3 (-1)+1=1^3
3 +( -2) =1

Ceci confirme que l'addition de la series* ne contient aucun nbr cube.
SERIES* 1+7+19+37+61+91......3 n^2+3 n+1 (nombres héxagonaux)
SOMME 1 8 27 ............ n^3
a^3+b^3=c^3 n'a pas de solution

Vous faites trop de suppositions non justifiées:
1) Soit c^3=a^3+b^3, a,b,c entiers naturels.
Vous ne justifiez pas pourquoi nécessairement c=a+1 ou b+1

2) Vous ne montrez pas correctement que l'équation 3 n^2+3 n+1=x^3
n'a comme seule solution n=-1, x=1.

[jean reaver]

qlq soit n,n+1 c'est le nbr qui vient après.
n=b et n+1 =c
c=b+1
c^3=b^3+?
(n+1)^3=n^3+(3 n^2+3 n+1)
(b+1)^3 ou c^3 puisque b=n

[eudea-panjclinne]

Si vous voulez montrer qu'il n'existe pas d'entier naturel a, b, c tels que c^3=a^3+b^3 et utiliser votre raisonnement vous devez montrer d'abord
pourquoi vous pouvez prendre c=a+1 ou c=b+1 et non pas supposer directement que c=n+1 et b=n.

[A voir en vidéo sur Futura]

[jean reaver]

ex:
c=5
c^2=5^2
5 c'est
(1+4)=5
(2+3)=5
(1+4)^2=4^2+(2*4*1+1^2)
(2+3)^2=3^3+(2*3*2+2+2^2)
25 = 9 + 16

c=b+1
c=b+2

la demonstration de 3*y^2+3*y+1=x^3 est suffisante .
https://www.wolframalpha.com/input/?...*y%2B1%3Dx%5E3
chercher step by step .c'est payant .

[jean reaver]

@ eudea
J'ai utilisé cette méthode pouvoir créer des algorithmes.Pour savoir si le théoreme existe?
En se basant sur les series et tester leur racines.
Power 2=2y+1
Power 3=3*y^2+3*y+1
Power 4=4*n^3+6*n^2+4*n+1
voici l'algo
rem fermat theorem
FOR y = 0 TO 10000
a=3*y^2+3*y+1
print a,a^(1/3)
next y
Le test continu à l'infini sans rien donner?
Il fallait recourir au démonstration, Pour conclure.

[jean reaver]

@eudea


1)si en prend un nombre b=2,on le met au carré b^2
b^2 +(2b+1)(gnomon)
on obtient un carré de côté b+1 que l'on nomme c
c=b+1
b=0, 0^2+2*0+1=1
b=1 ,1^2+2*1+1=4
b=2 ,
1+3+5+7+9
il suffit de trouver un x^2 dans cette série pour confirmer que le theorème
existe pour la puissance 2
chercher si (2b+1)=x^2

2)on continu POUR les autres puissances.n

[eudea-panjclinne]

J'ai utilisé cette méthode pouvoir créer des algorithmes.Pour savoir si le théoreme existe?

J'avoue que j'ai du mal à vous suivre dans vos calculs peu documentés.
Sachez, ce que vous savez peut-être, qu'un algorithme n'est pas une démonstration, implémenté dans un certain langage sur une machine, il vous donnera des résultats limités par les possibilités de la machine et/ou votre patience.

[jean reaver]

Voci l'image avec la tentative d'expliquer .

[jean reaver]

j'apporte ici la soution de 2n+1=x^2?
si x est impair on peut l'écrire 1-2m
x^2=4m^2+4m+1
=2 (2m² - 2m) + 1
=2n+1
et
4m^2+4m+1=2n+1
(4m^2+4m)=2n
(4m^2+4m)/2=n
2m^2+2m =n
2(m^2+m)=n

[jean reaver]

Vous faites trop de suppositions non justifiées:
1) Soit c^3=a^3+b^3, a,b,c entiers naturels.
Vous ne justifiez pas pourquoi nécessairement c=a+1 ou b+1

2) Vous ne montrez pas correctement que l'équation 3 n^2+3 n+1=x^3
n'a comme seule solution n=-1, x=1.

J'ai posté un schéma explique b+1
aussi la démonstration pour x^2
la même chose pour x^3
x=1-2m et n=2m^2-2m
ce genre de calcul existe déja en anglais.(hand right side).Donne toutes les solutions a^n+b^n=c^n