Bonjour j'ai un dm à faire sur les matrices assez compliqué pourriez vous me dire si ce que j'ai fait est bon et m'aider sur les questions où je bloqe
Partie I : Fonction homographiqueOn considère la fonction homographique définie par f(x)=ax+b/cx+d avec c≠0 et d ≠0.On suppose de plus que ad−bc≠0et que −dc<0.La fonction f est donc définie sur [0;+∞[ ( R + ) .On associe à f la matrice A=a b
. c d
1. Démontrer que le sens de variation de f dépend du signe du déterminant de A.
1j'ai fait la dérivé et ait obtenu ad - bc en numérateur donc c'est du signe du déterminant
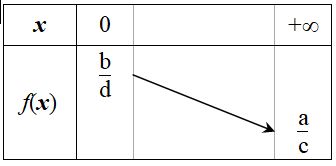
2. Démontrer que pour tout x réel, on a a/c⩽f(x)⩽b/d si f est décroissante ou b/d⩽f(x)⩽a/c si f est croissante.
2. j'ai completé mon tableau de variations et de 0 à + infini c'est décroissant avec b/d en limite en 0 et a/c comme limite en + infini , donc a/c<f(x)<b/d mais je sais pas comment justifier la deuxieme partie
PartieII: Approximation de √2√2est la solution positive de l'équation x^2−2=0(E).
1.Démontrer que (E)⇔x=x+2/x+1. Autrement dit, √2est solution de x=f(x)et fonction homographique.
1. j'ai isolé et fait les manifs et ait obtenu x²- 2 = 0 ce qui montre que racine de 2 est solution
2. Utiliser la partie I pour donner un encadrement de √2.3.
3 Calculer A2et A3et en déduire de nouveaux encadrements de √2
cependant pour les deux dernières questions je coince un peu
-----