Démonstration mathématique. Optique d'une antenne parabolique

[Yvan_Delaserge]

Bonjour,

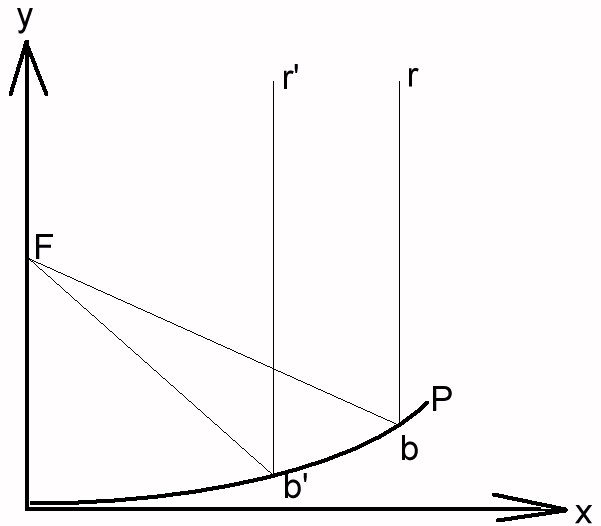
Sur ce schéma, la courbe P est une parabole, dont l'équation est y= c . X**2.

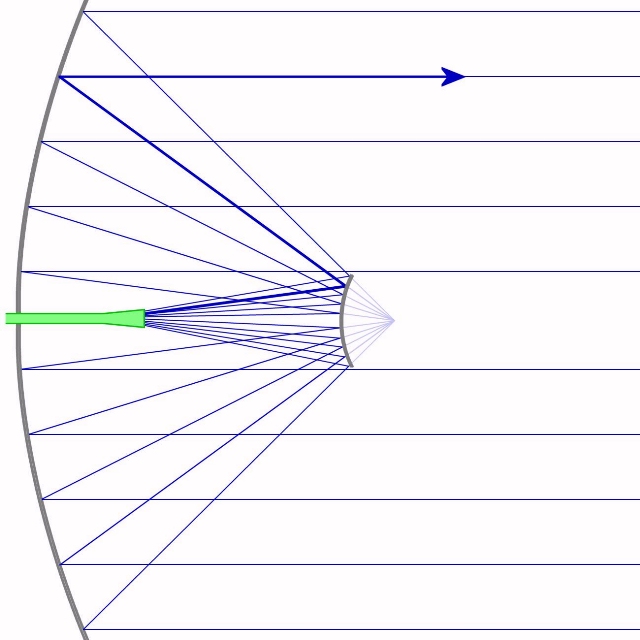
Cette courbe représente en coupe, un réflecteur parabolique d'une antenne.

Un rayon r, parallèle à l'axe y, va être réfléchi au point b, en direction du point F, qui est le foyer de la parabole. Il en va de même pour tout autre rayon parallèle à l'axe y.

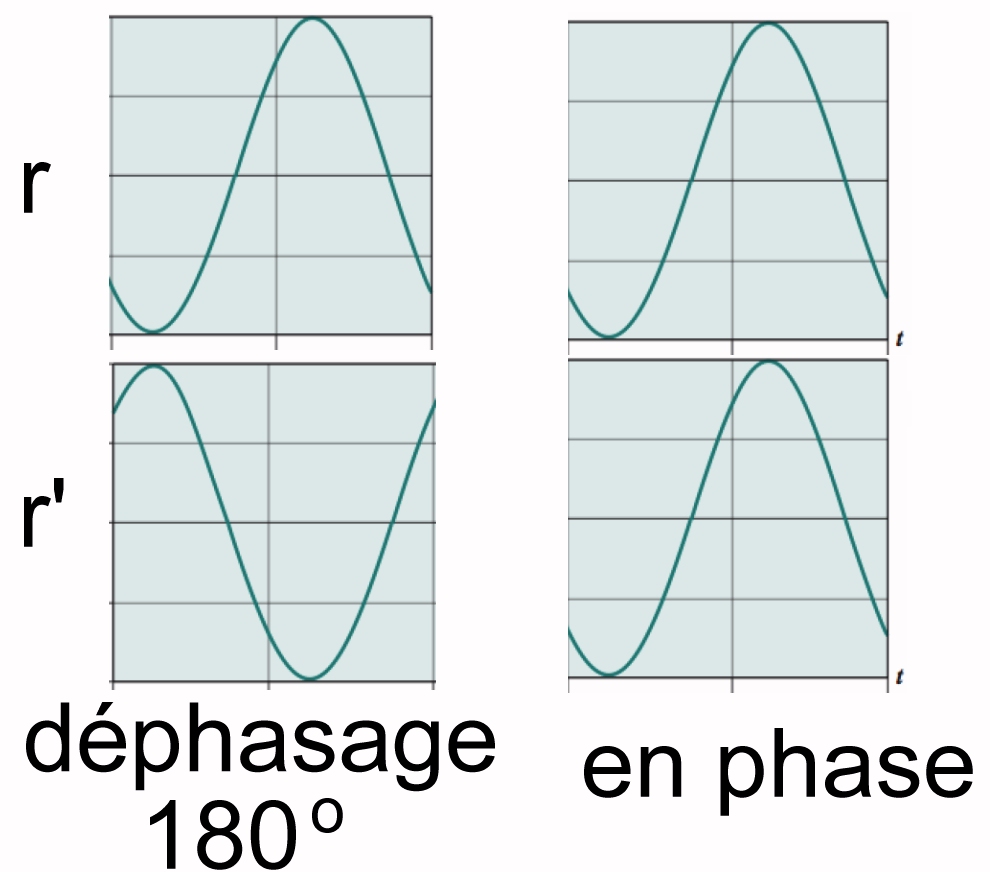
Peut-on démontrer mathématiquement (et si oui, comment?) que le chemin parcouru par tout rayon parallèle à r et réfléchi par la parabole, sera de longueur égale?

Merci d'avance et bonne soirée.
-----

[penthode]

hello ,

une parabole n'est pas un cercle !

donc les distance f-b , f-b' , f-b" , etc sont différentes

[invitedd63ac7a]

Je pense que @Yvan_Delaserge a oublier la directrice : voir définition d'une conique, en particulier parabole, par foyer et directrice.

[Yvan_Delaserge]

hello ,

une parabole n'est pas un cercle !

donc les distance f-b , f-b' , f-b" , etc sont différentes

Bonjour Penthode et merci pour ta reponse.
C'est vrai que b-f est plus long que b'-f, mais le rayon b a moins de chemin a parcourir que b' avant de rencontrer la parabole. Donc au total, les deux rayons auraient le meme chemin a parcourir. Du moins, c'est ce que j'aimerais demontrer.
Ce qui me fait penser que tel est bien le cas, c'est le raisonnement en termes de front d'onde plan, c'est-a-dire le cas d'une onde arrivant de tres loin.
Si ce front d'onde est perpendiculaire a l'axe de revolution de la parabole, chaque point du front d'onde va etre reflechi vers le foyer de la parabole, et va arriver au point F avec la meme phase, ce qui va permettre à l'antenne parabolique de présenter un gain. S'il y avait déphasage entre les différents points du front d'onde, l'énergie venant de certains points annihilerait celle d'autres points.
Pour que la phase soit la même au foyer, il faut que le chemin parcouru par chaque point du front d'onde soit identique.

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

Désolé de te décevoir, mais les longueurs que tu évoques ne sont pas égales (pour une onde plane perpendiculaire à l'axe du paraboloïde).
Attention aux fausses idées : "S'il y avait déphasage entre les différents points du front d'onde, l'énergie venant de certains points annihilerait celle d'autres points." Non, des énergies ne s'annulent pas additivement. Et il y a bien ici un gain en énergie, même si la phase est brouillée, perdue.

Pour comprendre pourquoi les distances ne sont pas égales, vois par exemple l'article parabole de Wikipédia, en particulier la définition géométrique par foyer et directrice, puis le paragraphe "tangente et bissectrice".

Cordialement.

[Yvan_Delaserge]

Bonjour.

Désolé de te décevoir, mais les longueurs que tu évoques ne sont pas égales (pour une onde plane perpendiculaire à l'axe du paraboloïde).
Attention aux fausses idées : "S'il y avait déphasage entre les différents points du front d'onde, l'énergie venant de certains points annihilerait celle d'autres points." Non, des énergies ne s'annulent pas additivement. Et il y a bien ici un gain en énergie, même si la phase est brouillée, perdue.

Pour comprendre pourquoi les distances ne sont pas égales, vois par exemple l'article parabole de Wikipédia, en particulier la définition géométrique par foyer et directrice, puis le paragraphe "tangente et bissectrice".

Cordialement.

Bonjour gg0 et merci de ta réponse.

Si deux ondes de même puissance interagissent en un point donné, elles peuvent être en phase (décalage = 0) ou décalées de x degrés.
Si le déphasage est nul, elles s'additionnent.
Si le déphasage est de 180 degrés, leurs effets s'annulent, car au niveau positif de l'une, correspond le niveau négatif de l'autre.



Mais il ne s'agit pas, bien entendu, d'une annihilation d'énergie, c'est une impossibilité physique. Je me suis mal exprimé, désolé.

Une application grand public de ce phénomène peut se trouver dans certains casques audio haut de gamme. Pour échapper au bruit extérieur, ils comportent un petit micro qui capte le bruit extérieur, un ampli qui introduit un déphasage de 180 degrés et un petit haut-parleur à l'intérieur du casque.
On les trouve sous la dénomination "noise cancelling headphone".

[gg0]

Oui, je connais tout ça. Les interférences destructives depuis plus de 50 ans .
A noter : Ça se passe en un point précis, le capteur d'une antenne n'est pas ponctuel.

[Yvan_Delaserge]

Je pense que @Yvan_Delaserge a oublier la directrice : voir définition d'une conique, en particulier parabole, par foyer et directrice.

Merci eudea-panjclinne de m'avoir mis sur la bonne voie.

Pour bien comprendre le fonctionnement d'un réflecteur parabolique, il faut modifier le schéma ci-dessus comme suit:

PARABOL2.jpg

Dans le cas particulier d'une parabole, MF = MH et SF = SK.

Fort bien, mais ce qui nous intéresse, dans le cas d'un réflecteur parabolique, c'est ce qui se passe devant la parabole, pas derrière.
On va donc tracer la ligne qui passe par A et A', parallèle à l'axe des x, (que l'on appelle la directrice, merci encore une fois à eudea-panjclinne).
AH = AH' = c, une distance arbitraire.
AM = c - MH et A'M' = c - M'H'.

On cherche à démontrer que AM + MF = A'M' + M'F. Cela démontrerait que les deux rayons r et r' parcourent la même distance.

Comment faire?

[mécano41]

Bonjour,

Une petite appli que j'avais faite il y a longtemps. J'ai ajouté la longueur du faisceau pour ton cas ; ça ne démontre pas mais ça peut aider....

Cordialement

[mécano41]

Une parabole est la courbe dont chaque point est à égale distance de la directrice et du foyer. La directrice est parallèle à l'axe x, à distance constante. Dans mon fichier, le point bleu est aussi à distance constante de l'axe x (donc à distance constante de la directrice). Dans ton dessin : FM=MH, FM' = MH', AH = A'H = constante. Tu peux en déduire ce que tu cherches, il me semble...

Cordialement

[gg0]

Bonsoir Yvan.

AM+MF = AM+MH=AH.

Finalement, j'ai raisonné à l'envers, tu avais raison.

Cordialement.

[Yvan_Delaserge]

Une parabole est la courbe dont chaque point est à égale distance de la directrice et du foyer. La directrice est parallèle à l'axe x, à distance constante. Dans mon fichier, le point bleu est aussi à distance constante de l'axe x (donc à distance constante de la directrice). Dans ton dessin : FM=MH, FM' = MH', AH = A'H = constante. Tu peux en déduire ce que tu cherches, il me semble...

Cordialement

Merci mécano 41, elle est bluffante, ton appli. Bravo!
Et en déplaçant le curseur, on constate que la distance parcourue (le "temps de vol" pourrait-on dire) de chaque point du front d'onde est rigoureusement identique. C'est exactement ce que je voulais savoir.

Merci encore, mécano 41!

En fait j'avais besoin de savoir ça parce que ce que je cherche à faire est un peu plus compliqué. Je m'explique:

Un ami m'a donné il y a longtemps une parabole, que voici:



Elle est de provenance inconnue et plutôt ancienne, mais elle n'a pas subi de déformations et c'est de la bonne ferraille galvanisée. Du solide. Elle présente un diamètre d'environ 1 m 50, donc elle serait intéressante à utiliser.
C'est ce que j'ai essayé de faire en calculant la distance focale avec la formule f= D**2/16c (où D est le diamètre et c la profondeur du réflecteur) et en y plaçant un LNB satellite, comme on le voit sur la photo.
Hélas, ça marche très mal. Mon ami m'a dit qu'il était arrivé à la même conclusion. C'est du reste parce qu'il ne pouvait rien en faire qu'il me l'a donnée!

Mon hypothèse est que ce réflecteur n'est pas parabolique mais sphérique. La large découpe circulaire au fond de la parabole sert à y placer un sous-ensemble (que je ne possède pas), constitué d'un réflecteur secondaire hyperbolique et d'un illuminateur. C'est ce que l'on appelle une antenne Cassegrain.

Pour pouvoir utiliser cette parabole, il faudrait que je réalise un sous-réflecteur avec la forme adéquate.
Le diamètre du sous-réflecteur est déjà défini. Il sera le même que celui de la découpe du fond de la parabole. Reste à déterminer la forme.

Je vais commencer par faire un relevé de la profondeur de chaque point de ma parabole (axe y), le long d'un diamètre (axe x) et en utilisant ton appli, remplir les cellules des colonnes B et C, lignes 42 à 92.

De cette manière, même si l'on n'a pas affaire à une parabole, mais à une sphère, comme ton application calcule les tangentes pour déterminer les réflexions, elle me montrera à quel endroit (point rouge) chaque rayon incident est réfléchi.

C'est bien exact? Ou bien est-ce que l'appli ne fonctionne que pour une parabole?


Le sous-réflecteur de l'antenne Cassegrain devra être placé à une hauteur telle qu'il intercepte tous les rayons réfléchis par le réflecteur primaire.

Il ne restera plus qu'à calculer la forme de la surface du sous-réflecteur. On sait seulement que cela doit être une hyperbole,

Est-ce que tu as aussi une appli qui serait capable de calculer la forme d'un sous-réflecteur d'une antenne Cassegrain?

[albanxiii]

Bonjour,

Si deux ondes de même puissance interagissent en un point donné, elles peuvent être en phase (décalage = 0) ou décalées de x degrés.
Si le déphasage est nul, elles s'additionnent.
Si le déphasage est de 180 degrés, leurs effets s'annulent, car au niveau positif de l'une, correspond le niveau négatif de l'autre.

Ceci n'est pas vrai ici puisque vous n'êtes pas en situation d'interférences. Il n'y a aucune relation de phase entre les faisceaux qui convergent vers le foyer.
Pour que des ondes interfèrent elles doivent êtres cohérentes. Autrement dit, une onde n'interfère qu'avec elle même (cf. les dispositifs interférentiels classiques, Michelson = division ou miroir de Fresnel).

Ici, ce sont les puissances qui s'additionnent.

[Yvan_Delaserge]

Pour référence, une antenne Cassegrain.



En réalité, dans l'antenne Cassegrain, le réflecteur primaire (le plus grand des deux, concave) est parabolique (et non pas sphérique), le secondaire (convexe) est hyperbolique.

Le foyer du réflecteur secondaire se trouve derrière lui (c'est-à-dire du côté concave).
On place le réflecteur secondaire de manière à ce que son foyer se trouve au même endroit que le foyer du réflecteur primaire.


Mais qu'en est-il d'un réflecteur sphérique?

On pourrait même imaginer un réflecteur primaire de forme ni exactement parabolique, ni exactement sphérique. Une appli analogue celle de mecano permettrait de définir la forme que devrait avoir le réflecteur secondaire pour que les trajets (jusqu'à l'illuminateur) de tous les rayons incidents parallèles à y, aient exactement la même longueur.

Avantage: Une fabrication du réflecteur primaire moins chère, puisque moins précise. Compensée par un réflecteur secondaire de forme plus élaborée, destinée à compenser les aberrations. Comme le réflecteur secondaire est plus petit, il est moins onéreux à fabriquer.

[mécano41]

Bonjour,

...C'est bien exact? Ou bien est-ce que l'appli ne fonctionne que pour une parabole?

Oui, j'avais fait cela pour expliquer à quelqu'un comment un rayon se réfléchissait sur un miroir parabolique.

Cordialement

[Yvan_Delaserge]

Bonjour,


Ceci n'est pas vrai ici puisque vous n'êtes pas en situation d'interférences. Il n'y a aucune relation de phase entre les faisceaux qui convergent vers le foyer.
Pour que des ondes interfèrent elles doivent êtres cohérentes. Autrement dit, une onde n'interfère qu'avec elle même (cf. les dispositifs interférentiels classiques, Michelson = division ou miroir de Fresnel).

Ici, ce sont les puissances qui s'additionnent.

Bonjour albanxiii.

La cohérence temporelle d'une onde est liée à la largeur de bande spectrale de la source. Une onde réellement monochromatique (une seule fréquence) aurait, en théorie, un temps et une longueur de cohérence infinis.

Dans l'interféromètre de Michelson, on sépare le signal issu d'une source unique, cohérente, en deux parties et on allonge ou on raccourcit le trajet que parcourt l'une des deux parties, avant de les recombiner. Si la différence de trajet introduit un déphasage de 180 degrés, les deux ondes s'annulent. Si le déphasage est nul, elles se renforcent.

Dans le cas d'une antenne parabolique, qui reçoit un signal en provenance d'une source unique, cohérente et éloignée (par exemple une antenne parabolique de réception satellite), le front d'onde va être plan. La phase ne va-t-elle pas être la même sur tout le front d'onde?

[apprenant]

BONJOUR MECANO41 j'ai telechargé votre application excell pour le calcul de la distance focal.. peux tu stp le modifier pour une etude que je suis entrain de faire avec un parabole de diamètre 131 cm et une profendeur de 38 cm.

merci

cordialement

[mécano41]

Bonjour,

Il te suffit de modifier les deux cellules jaune en haut à gauche et y mettre :

- diamètre : 1310 mm
- hauteur : 380 mm

puis bouger le curseur si tu veux faire varier la position du rayon incident.

Cordialement

[apprenant]

bonjour merci. c'est fait et c'est vraiment efficace merci.

je suis entrain de mener une étude sur les cuiseurs solaires paraboliques, j'ai donc trouver très efficace votre travail ce fichier. je voulais savoir si c'est possible de modifier ce fichier afin d'ajouter plus de rayon incident et d'autres paramètres comme le système de suivi du soleil et l'évaluation de la température en vue d'une utilisation optimale du dispositif.

[apprenant]

bonjour merci. c'est fait et c'est vraiment efficace merci.

je suis entrain de mener une étude sur les cuiseurs solaires paraboliques, j'ai donc trouver très efficace votre travail ce fichier. je voulais savoir si c'est possible de modifier ce fichier afin d'ajouter plus de rayon incident et d'autres paramètres comme le système de suivi du soleil et l'évaluation de la température en vue d'une utilisation optimale du dispositif.

[mécano41]

Bonjour,

Tu peux aller voir ce que nous avions fait ici : https://forums.futura-sciences.com/m...u-solaire.html
Cela ne fonctionne que si tu as une version EXCEL sur PC et il faut autoriser les macros à l'ouverture car code VBA.

L'appli permet de faire varier les angles d'un panneau solaire et une visualisation en 3D permet de changer les angles de vue. Regarde si tu peux en tirer quelque chose. Lis le sujet indiqué mais utilise le fichier joint (il est probable que j'ai modifié des bricoles par rapport au précédent)...Ce n'est pas simple...je n'ai pas trop envie de replonger là-dedans!

Cordilement

[apprenant]

bonjour, merci pour le travail et le temps disposé.