Bonjour.
Ce que cherchent moulte personnes un peu mathématiciennes et qui s'intéressent à l'angle d'incidence des rayons solaires sur un panneau solaire :
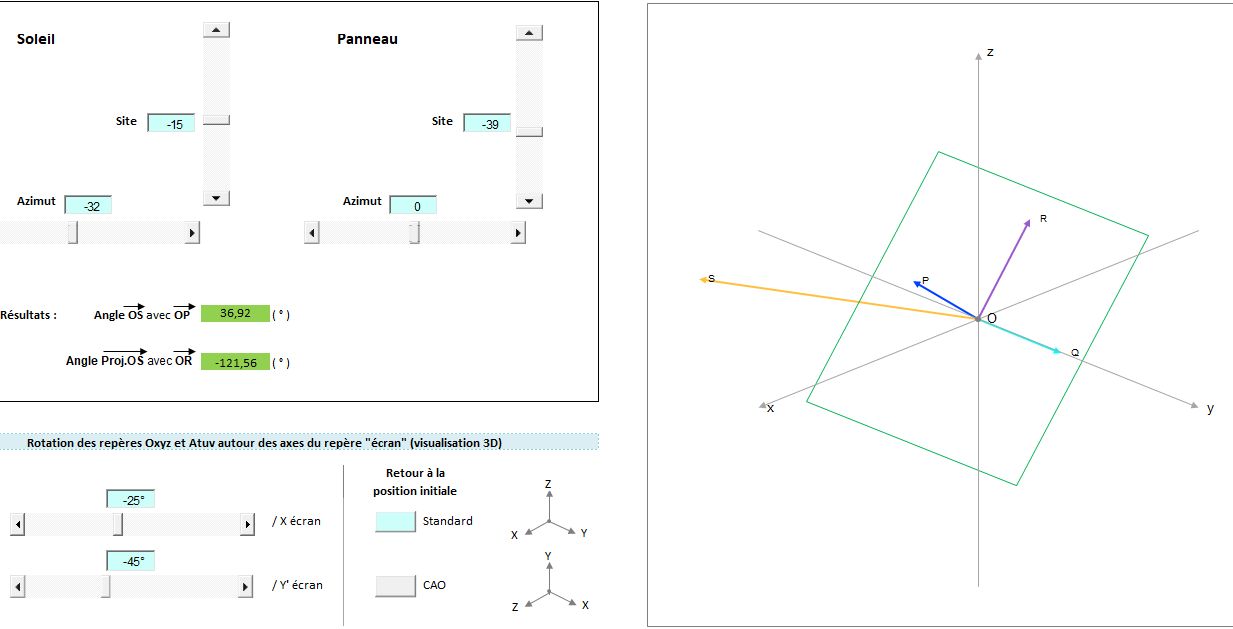
1) L'angle d'incidence d'un rayon solaire sur une surface plane (un panneau solaire),
2) et l'orientation d'un plan contenant ce rayon solaire, plan qui est perpandiculaire à ce panneau solaire [soit deux angles par rapport à l'un des deux axes carthésiens se situant dans le plan du panneau solaire et par rapport à une normale] ?
Il faut tenir compte en plus d'un tout premier plan, le plan horizontal sur lequel est positionné de manière fixe ledit panneau solaire. Car l'on dispose d'abord des angles de rayonnement solaire a' et b' caractéristiques de l'endroit où se trouve le panneau solaire (la latitude, l'heure de la journée, le décalage horaire par rapport au méridien, le décalage horaire saisonnier (heures d'hivers et heures d'été), ...).
Il s'agit d'un contexte à deux coordonnées polaires.
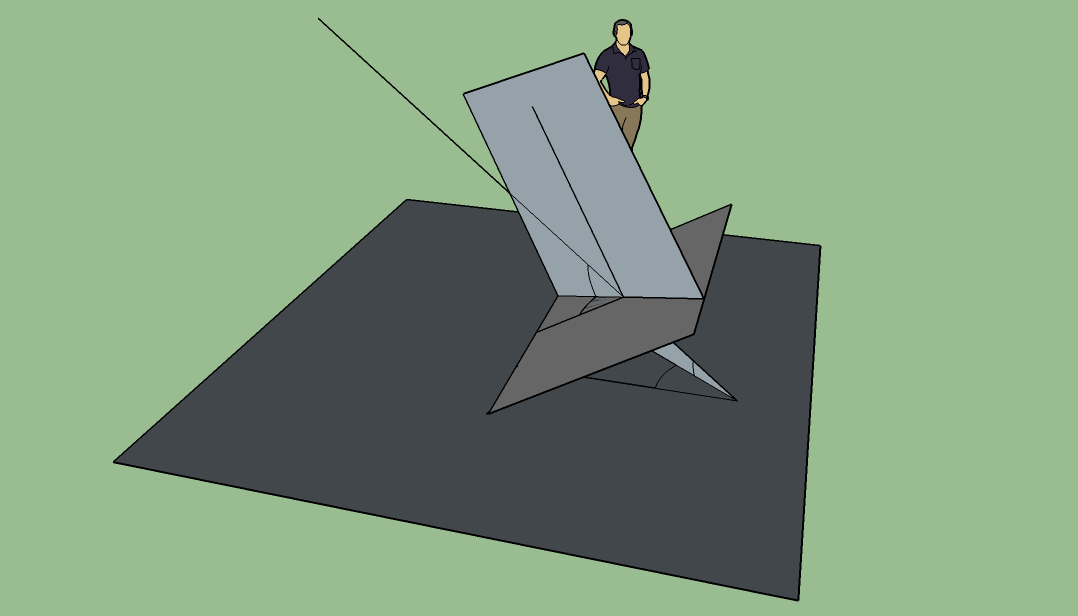
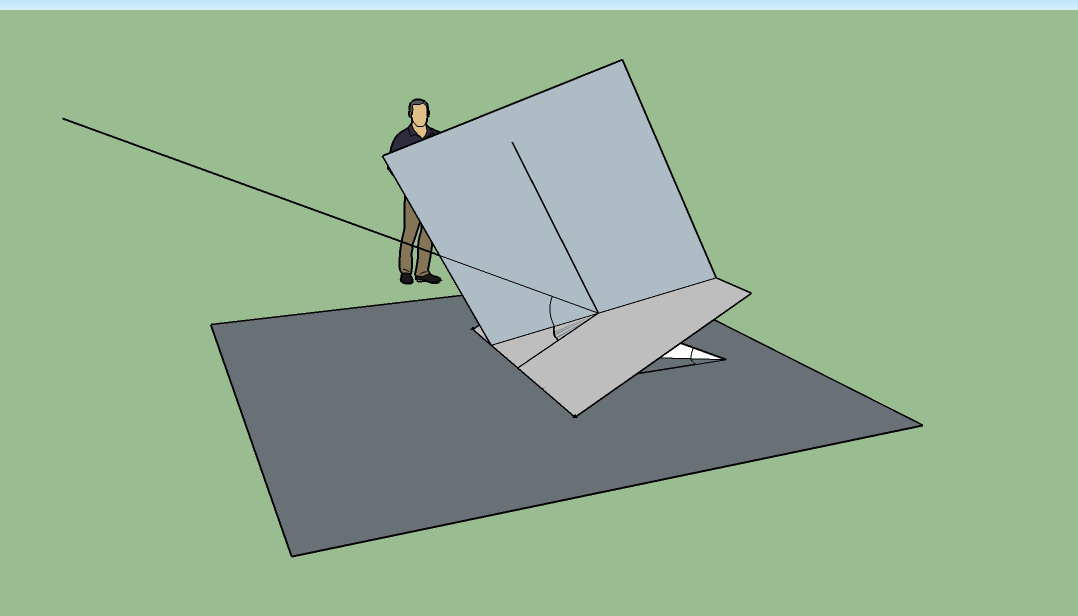
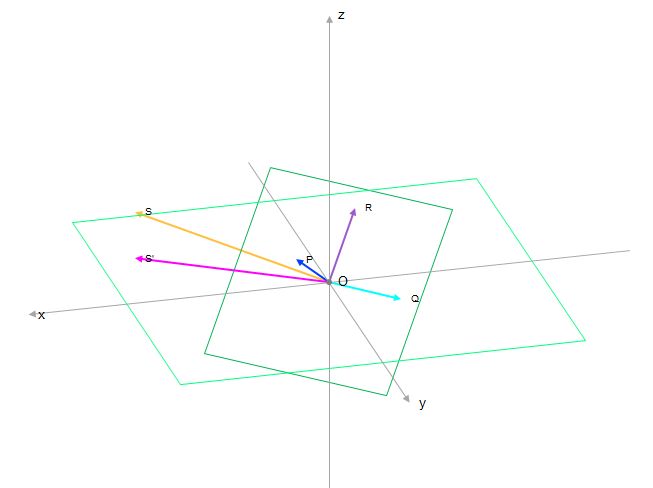
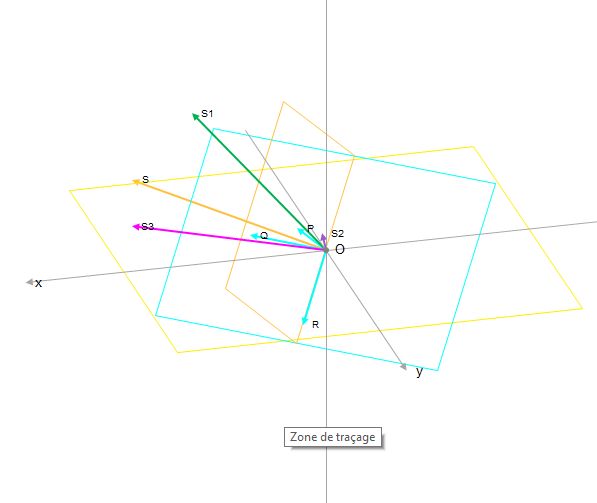
Mon dessin 3D montre les trois plans, les deux droites de référence (dirigées vers le Sud) sur le panneau solaire et sur le plan horizontal, un rayon solaire incident ainsi que
- les deux angles d'incidence a" et b" par rapport au panneau solaire
- les deux angles d'incidence a' et b' par rapport au plan horizontal
Quelqu'un peut-il me renseigner une adresse URL où l'on trouve les formules mathématiques de ce système ?:
a" = f(a', b', c) et b" = f(a', b', c)
c: Angle d'inclinaison du panneau solaire par rapport à la verticale.
Bien à vous et merci d'avance.
-----