Corrélation entre deux égalités

[Random9]

Bonsoir,
Je suis sur un livre de physique (Le merveilleux "Pourquoi e=mc² et comment ça marche ?" de Brian Cox et Jeff Forshaw).
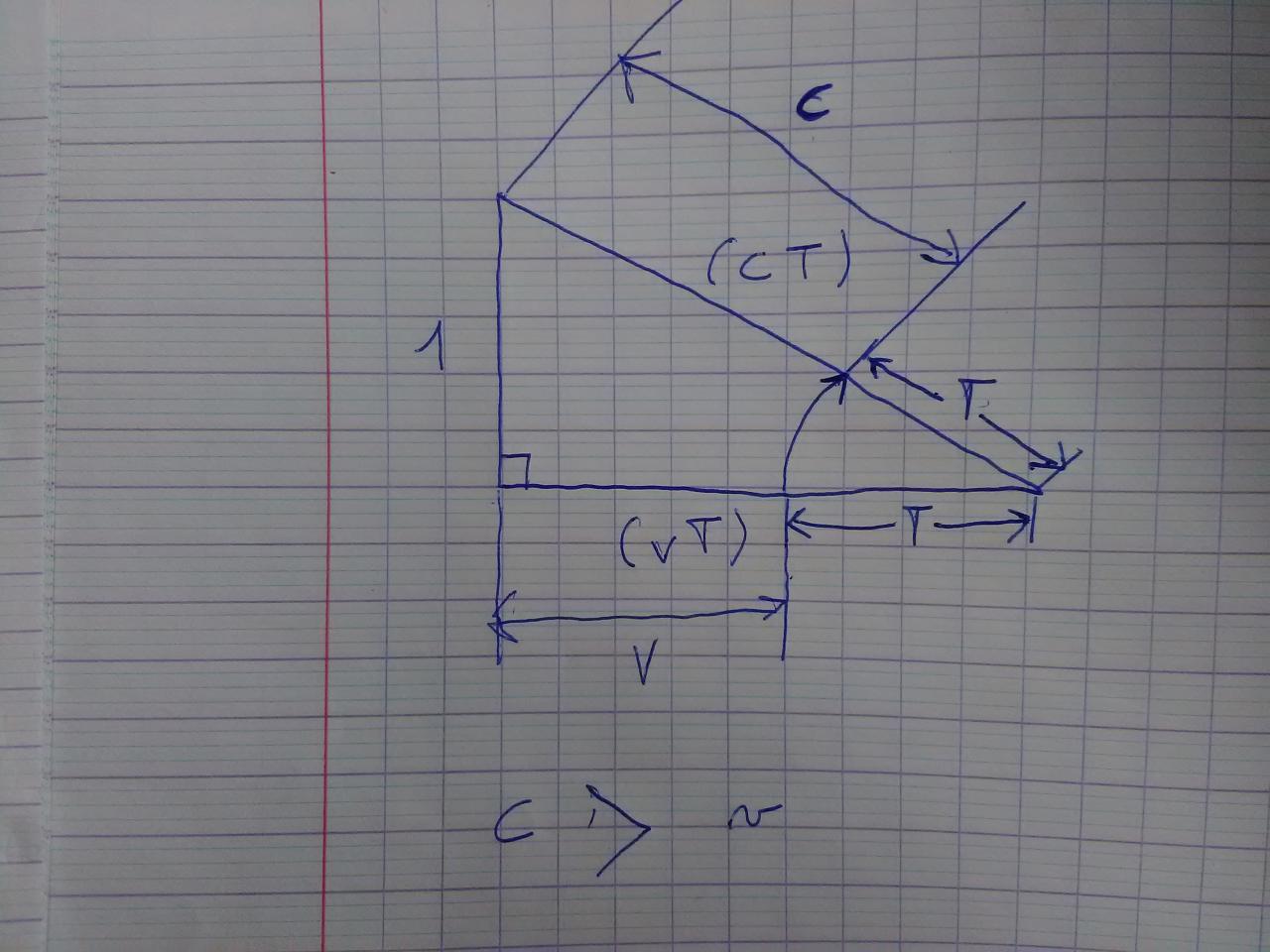
A un passage du livre, un simple théorème de Pythagore est utilisé :

cT² = 1² + vT²

L'auteur en déduit :

T² = 1/(c²-v²).

J'ai compris le passage mais impossible pour moi de trouver la corrélation pour passer de l'étape 1 à la 2 d'une manière mathématique.
Mon actuel niveau en maths (4eme) et le fait que je ne sache pas de quelle notion il s'agit font que je suis incapable de résoudre ceci.
Merci de votre lecture.
-----

[albanxiii]

Bonjour,

Le mot corrélation est inadapté. On passe simplement d'une relation à l'autre par des manipulations de base : ajouter ou retirer la même quantité aux deux membres, multiplier ou diviser les deux membres par la même quantité (non nulle en cas de division).

Même en 4ème on doit savoir faire ça.
(cT)^2 = 1 + (vT)^2 (sinon la relation n'est pas homogène)
donc
c^2T^2 - v^2T^2 = 1
donc
T^2(c^2 - v^2) = 1
et le résultat final s'ensuit si c^2 - v^2 n'est pas nul.

[Random9]

Salut, merci de ta réponse.
Je sais bien que je suis censé le savoir mais il y a beaucoup de notions que l'on n'a pas abordé cette année et que l'on était censé voir, j'essaye de rattraper ce retard.

Mais en tout cas merci pour la solution !

[albanxiii]

j'essaye de rattraper ce retard.

Bon courage alors !
Le secret pour s'améliorer : s'entraîner, c'est à dire faire des exercices, plein. (c'est la même technique que les sportifs de haut niveau... ils s'entraînent, beaucoup, et intelligemment, mais beaucoup !)

Donc, assurez vous de savoir le refaire tout seul.

[A voir en vidéo sur Futura]

[Random9]

En fait en y allant étape par étape j'ai retrouvé le résultat... C'était sûrement à cause de l'heure :'D
En tout cas merci pour ces précieux conseils.

[jeanbon22]

Bonjour,

Pythagore c'est simple, mais très important, c'est le socle de toutes les mathématiques. Tous les problèmes analytiques ne sont qu'une déclinaison de la géo métrie. La mesure de la terre(du cercle).

N'hésite pas à transposer toujours les équations en géométrie. Surtout quand cela est précisé comme dans le problème. Comme le schéma ci dessous.



Et là tu pourras aussi constater que C-v, ne peut pas être nul si on emploi Pythagore. Tout l'algèbre, les équations te seront beaucoup plus simple, si tu les transposes toujours en forme géométrique. Et cela te sera très utiles en trigo, dérivée.... Si tu continues dans la voie E=mC².

Erratum, il y a une petite erreur dans les schéma, pas l'idée. Mais la représentation de C et v est fausse.

[Random9]

Merci du conseil !

En fait cT est la la vitesse de la lumière multipliée par un temps donné, et vT une variable qui représente une vitesse différente multiplié par ce même temps, ce qui permettrait de mesurer au final la valeur de T en fonction de v.
Le 1 est assez arbitraire et j'aurai plutôt dû le déclarer comme inconnu histoire d'avoir la formule quelque soit la valeur présente.

En fait, le sujet est un train se déplaçant à la vitesse v dans lequel se trouve deux miroirs séparés par une distance d (Le fameux 1 dans la formule)
Un photon rebondit entre les deux et le temps d'un passage à un autre du miroir est T.
Le raisonnement est un peu à l'envers : On sait d'origine que T est différent entre un référentiel où l'observateur est à l'intérieur du train et un autre ou l'observateur est à l'extérieur, vu que de l'extérieur le photon aura une distance plus grande à parcourir à cause
de la distance rajoutée par le parcours du train, et tout ça permet de mesurer la dilatation temporelle simplement avec un théorème de Pythagore, je trouve ça génial !


Mais le fait de le transposer géométriquement est bien plus intuitif dans une telle situation avec trente six mille inconnues ce qui change un peu des exercices que j'ai eu cette année...
Bonne journée !