Bonjour!
Est)ce que vous pouvez m'aider pour la résolution de cet exercice svp?
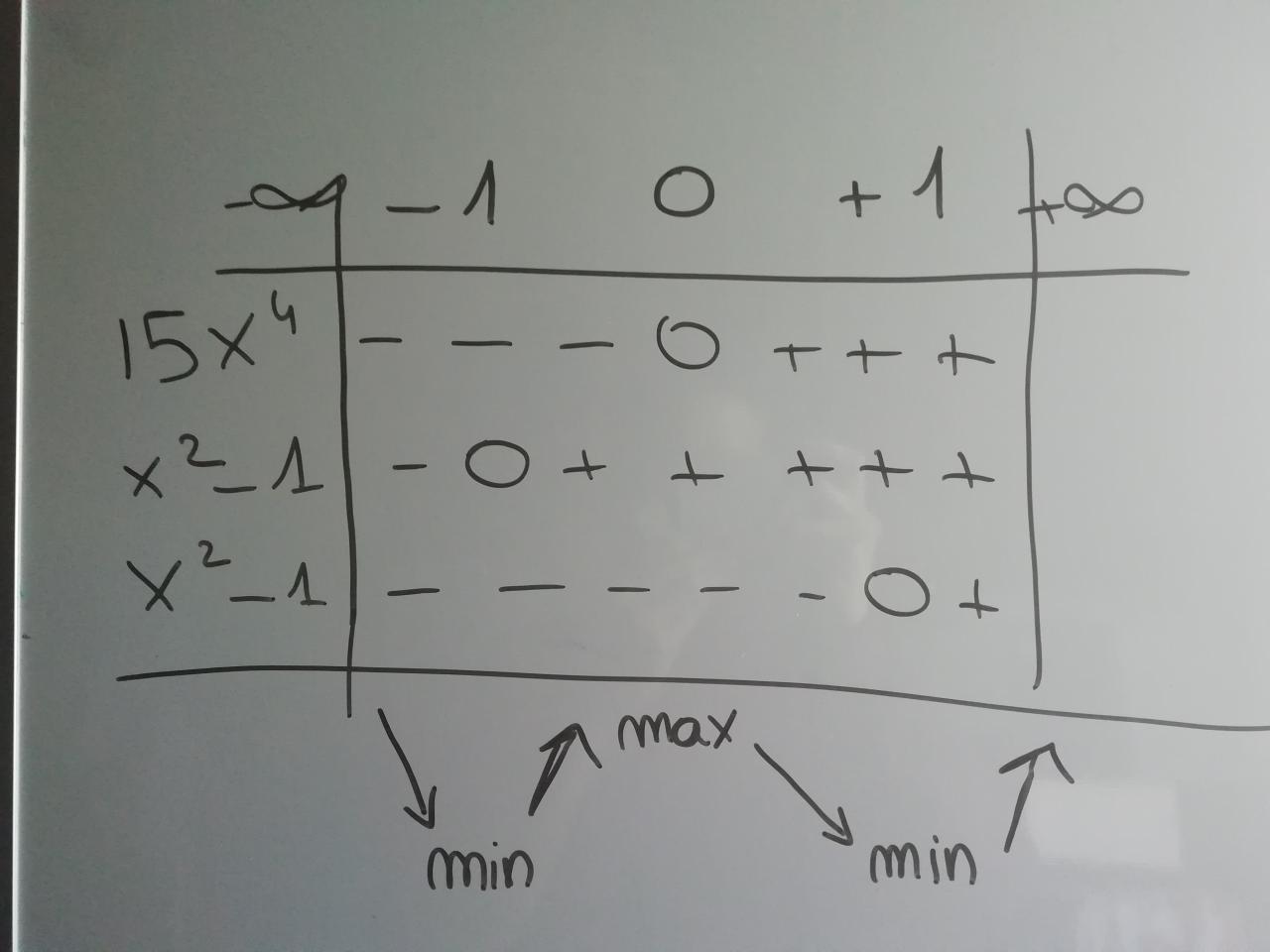
Soit la fonction f(x)=3x^5 - 5x^3. Combien d'extremums locaux possède-t-elle?
J'ai procédé en faisant la dérivé de f(x) et j'obtiens 15x^2(x^2 -1) donc les points critiques que j'ai trouvé sont 0, 1 et -1. Je trouve donc 3 réponses et je ne comprend pas pourquoi la réponse est 2. Je suppose qu'il y a un point d'inflexion du coup? Mais comment sait-on si on a un point d'inflexion ou pas?
Je vous remercie d'avance
-----