"Chanceux" d'Euler: il a pensé à quoi en fait?

[invite84127968]

Mes deux précédents posts n'ont appelés aucunes réponses car trop triviaux (c'est un de mes problèmes avec une capacité à la dispersion trop importante).
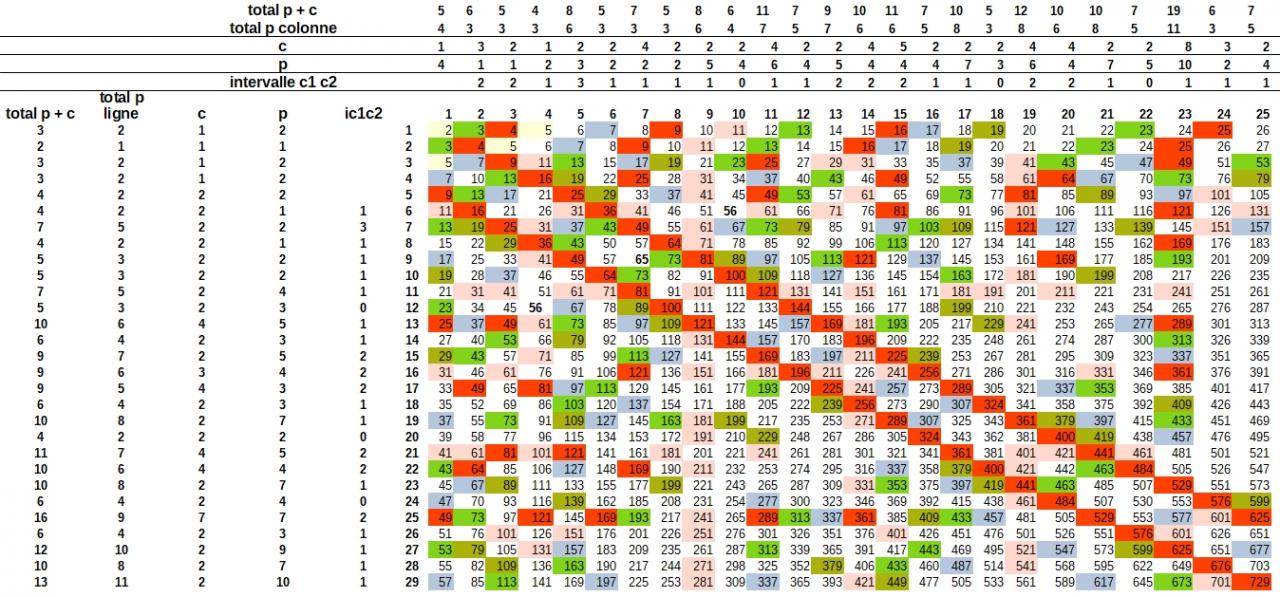
J'ai donc pris un peu de temps pour transformer les suites de résidus de la division euclidienne et fais une conversion qui me ramène à une série de suites intégrant les nombre promiques et carrés. Ensuite j'ai fait la somme cumulée des termes et j'obtiens ce tableau:
imp2 2.jpg


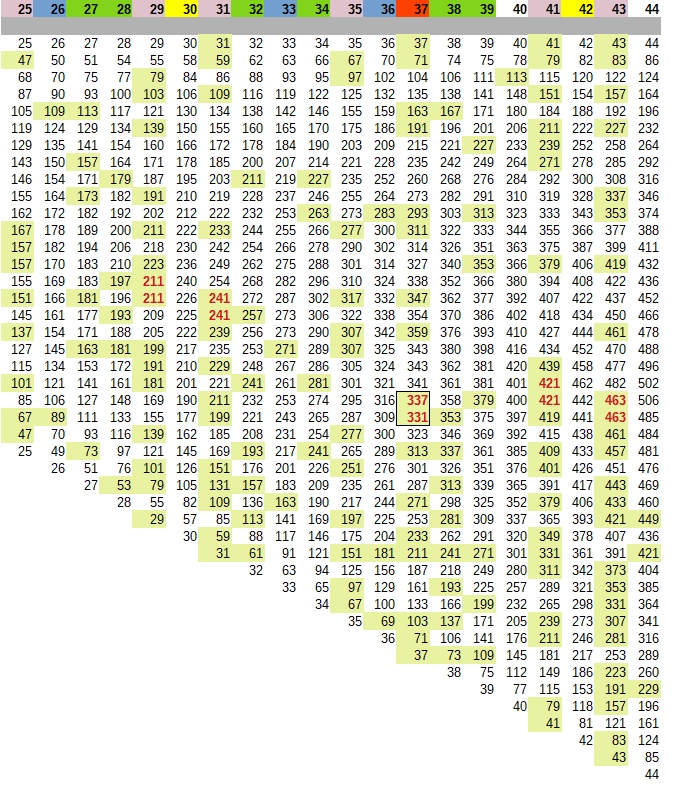
J'ai marqué en jaune les premiers et en couleurs différentes les suites de type n*(2*n+1),n*(3*n+1) etc... le nombre de premiers en colonne sur un échantillonnage faible est supérieur dans les colonnes avec un nombre premier, que le nombre de nombre premiers de la colonne soit le cumul de tous ces nombres premiers ou celui des premiers distincts entre eux. A noter les colonnes 13 , 17 et 38. La division par 5 et 7 de la colonne 35 donne cela:
35.jpg

Du coup je me suis penché sur l’addition x+k*(x-1)= un nombre premier P(x). Les résultats de P(x) sont proportionnellement à x très bas: il y a des études à ce sujet?
-----

[ansset]

Mes deux précédents posts n'ont appelés aucunes réponses car trop triviaux (c'est un de mes problèmes avec une capacité à la dispersion trop importante).

je suppose plutôt ( en tout cas c'est mon cas ) qu'on ne comprend pas bien ce que tu fais.
en donc surtout ce que tu cherches à établir.
Cdt

[albanxiii]

Bonjour,

Mes deux précédents posts n'ont appelés aucunes réponses car trop triviaux

Ça n'est pas une raison pour oublier d'être poli.

Sur le fond, ansset a répondu. J'ajoute pour ma part que vous donnez l'impression d'avoir une attitude qui consiste à dire "J'ai pensé à ceci, ou cela, mais je n'ai pas envie de me creuser plus la tête. Pourriez-vous me dire si cela a un intérêt ?".
C'est pas comme ça que les choses fonctionnent.

[invite84127968]

Bonjour,



Ça n'est pas une raison pour oublier d'être poli.

Sur le fond, ansset a répondu. J'ajoute pour ma part que vous donnez l'impression d'avoir une attitude qui consiste à dire "J'ai pensé à ceci, ou cela, mais je n'ai pas envie de me creuser plus la tête. Pourriez-vous me dire si cela a un intérêt ?".
C'est pas comme ça que les choses fonctionnent.

Désolé je ne suis pas explicite dans mes formulations et je m'excuse si ma remarque semble impolie, je prépare une réponse détaillée mais je ne peux pas la produire rapidement:
Voilà le début de ma démarche en étapes, les motivations derrière chaque étape pourront être expliquées ensuite:

ec1.jpg

(car somme des restes n'ai pas un indicateur valide des nombres premiers)

ec2.jpg

Puis

ec3.jpg

Je prépare la suite de la description...

[A voir en vidéo sur Futura]

[invite84127968]

Dans ces suites j'ai observé:

- la somme en colonne des premiers est (x^2-x+4)/2

On les distingues donc facilement :

ec3 graph.jpg

La somme des x+1 premiers termes de ces suites sont de la forme a(n) = n*(n+1) puis la somme des x suivants restent de type n^2 :

ec3 obs.jpg

En faisant des sommes partielles entre les nombres premiers dans ce tableau j'ai remarqué une disposition des premiers et des carrés:

Sommes partielles entre p.jpg

de là j'ai eut l'idée d’additionner les termes des suites obtenues du tableau "écart entre les écarts" pour arriver aux suites décrite en post 1.

(Je continue les explications un peu plus tard.. le temps de créer les images etc..)

[invite84127968]

Autre illustration dans le tableau "écart entre les écarts",je vais le noté tableau EEE (pour la suite) il est possible de calculer la somme des colonnes pour les premiers, celle des non premiers n'est pas une formule unique, ce qui s'illustre aussi par le calcul d'une somme effective et d'une somme théorique si l'écart est nul alors le nombre considéré est premier :

Pièce jointe 395592 , à noter qu'il y a d'autres éléments à développer au sujet de ce tableau (notamment le fait que les colonnes des premiers ont une structure identique mais ne sont pas de même nature, à mes yeux il s'agit de combinaisons de termes qui se suivent de la même manière mais n'ont pas la même origine structurelle)

Enfin le tableau avec la somme des termes des suites obtenues du tableau "écart entre les écarts" noté tableau SEEE, donne une répartition de nombres premiers en colonne qui correspond au fait que la n-ème colonne est un nombre premier ou non, tout au moins sur l'échantillon considéré, je n'ai pas été très loin (109) , j'en suis à la recherche d'une compréhension de la structure obtenue.
Dans ce tableau les nombres premiers en colonne se répartissent de différentes façons mais ces "façons" se répètent (marquage des typologies par couleur sur la 1ère ligne)



... je continue

[invite84127968]

Le fait que le tableau SEEE intègre les suites de type n*(2*n+1),n*(3*n+1)... m'a ramener à la formule du chanceux d'Euler n (n+1) + 41 qui du coup ne me semble peut-être pas si chanceux.
J'ai donc entamer l'étude des suites x+k*(x-1)= un nombre premier P(x) pour voir, le couple x,x-1 de départ détermine déjà une partie de la structure de EEE. et donc voilà le pourquoi de ma question.

[invite84127968]

Pour illustrer voilà à quoi ressemble les suites x+x-1 avec x =8 on a 8,8+7,8+7+7,8+7+7+7 etc..

J'en tire le tableau suivant:


On remarque en diagonale deux lignes de carrées consécutifs (les carrés sont en rouge, les premiers sont toutes les autres couleurs), j'ai fait le compte en colonne et en ligne dans ce tableau du nombre de premier entre le premier terme et le premier carré (p), entre le premier et le deuxième carré ( ic1c2 en lignes et intervalle c1c2 en colonne ), le nombre de carré, puis le nombre totale de premiers et premiers + carrés.. je retrouve bien une liaison avec les premiers ordonnés.

Voilà, je ne sais pas si cette "corrélation" est étudiée quelque part, j'espère que ma question est cette fois plus compréhensible.

[invite84127968]

Bonjour je ne sais pas si mes explications ont été bien explicites ?

J'ai calculé les taux de premiers en colonne du tableau du post 1 (SEEE):



De n=5 à 109 cela donne:
Taux moyen de 22% de premiers pour toutes les colonnes de n=5 à 109
taux de 33% pour les colonnes avec n impaires et taux de 44% pour les n premiers.
L'idée est de savoir si la tendance dominante des taux s'amenuise en passant vers des grands nombres.
A noter le nombre 89 qui à un taux déjà inférieur à deux de ses encadrants non premiers 85 et 91.

[invite84127968]

Le tableau dans mon dernier message est illisible...

tx2.jpg