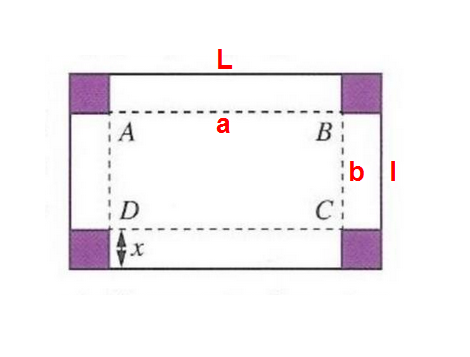
Bonsoir, j’essaye de comprendre cette exercice mais je n’arrive pas à percevoir la ‘’logique’’ de ce dernier ...
1) Comment trouver l’intervalle I, quel est la méthode ! (Dans ma tête c’est le vide)
2) Comment on trouve V(x)= 4x3-130x2+1000x ?? (Longueur*largeur*hauteur ?)
3) Là je comprends enfin quelque chose: Il faut faire un tableau de variations ! Mais je ne connais pas l’intervalle I...
Merci si quelqu’un a le courage de m’aider .
Bonjour.
Pour bien comprendre ce qui se passe, tu peux faire un modèle à l'échelle 1/2 : Tu découpes dans une feuille un rectangle de 20x12,5, tu lui enlèves des carrés dans le coins, tu plies suivant les pointillés, à 90°, et tu as la boite (pas fermée en haut). Après, si tu n'es pas totalement idiot, tu pourras facilement trouver quelles longueurs de côtés de carrés tu aurais pu prendre.
Quoique ... ton "(Dans ma tête c’est le vide
Cordialement.
Dernière modification par gg0 ; 12/12/2019 à 22h02.
Dans quel intervalle x peut-il varier ?
- considère le cas x = 0 : est-ce possible ?
- fais augmenter x petit à petit. imagine ce que devient le dessin avec les zones mauves à découper. Tu verras qu'il se passe quelque chose, à partir d'une certaine valeur de x, qui empêche de découper les carrés.
Justifier la formule de V(x).
Un volume d'une boîte c'est Longueur*largeur*hauteur évidemment ! Que veux tu que ce soit d'autre ?
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
Bonjour, -
Ne pourrais-tu pas commencer par exprimer les dimensions (a, b) du rectangle de base (ABCD) ?
Cela te permettrait de passer à son aire (S), puis au volume de la boîte ... et de répondre naturellement aux questions de l'exercice.
Bonsoir merci de m'avoir aidé et désolé de répondre que maintenant mais voici mes recherches :
Pour le Volume
-L*l*h=Volume boîte
-40*25*x= Volume
Pour l'aire du rectangle ABCD
-(L-2x)*(l-2x)=Aire ABCD
-(40-2x)*(25-2x)= Aire ABCD
Constitution de V (x):
1000x provient du volume (40*25*x)
Pour 4x au cube et -130x au carré je n'ai aucune idée .
Bon finalement je ne vois pas l'utilité de mes recherches pour répondre aux questions....
Merci d'avance à la personne qui aura encore le courage de m'aider
Ben tu y es presque
tu as trouvé l'aire du carré ABCD : (40-2x)*(25-2x)= Aire ABCD
Je pense que tu ne visualises pas la boite ... le fond de la boite c'est ABCD
La hauteur de la boite c'est ?
Bonjour, pour moi la hauteur c’est juste x mais je ne vois pas comment trouver cette intervalle I demandé...
Par contre en développant (40-2x) (25-2x) je trouve 4x2-130x +1000, ceci ressemble très fortement à V(x)= 4x3-130x2+1000x où il faut faire *x pour retrouver le volume dit dans l’énoncé.
Merci en tout cas pour votre aide
Dernière modification par Lachimiecphysique ; 15/12/2019 à 10h51.
donc tu trouves l'aire de la base ABCD de ta boite = 4x2-130x +1000
et tu sais que la hauteur est H = x et tu ne vois pas comment tu arrives au volume 4x3-130x +1000x ? ...
I c'est l'intervalle possible des x , par exemple si x = 30 tu vois bien que c'est pas possible car ton carton fait 40x25 ...
Bonjour, merci pour votre réponse.
Cela va vous paraître bizarre mais je ne vois pas vraiment pourquoi x=30 est impossible... (Peut être parce que la largeur qui est égal à 25cm n’est pas égal à 30cm *2..)
Mais j’ ai essayé de chercher:
Largeur = 25 cm= 12,5*2 cm où (25-2*12,5)
Donc x[0;12,5] ?
Merci pour votre aide
Bonjour.
As-tu déjà essayé de découper un carré de 30 cm de côté dans un rectangle de 20 cm sur 12,5 ?
Sérieusement, as-tu lu l'énoncé ? Lu pour comprendre ce qui est dit, pas pour poser des mots les uns à côté des autres sans lien entre eux ? Pourrais-tu te décider à agir intelligemment ?
Cordialement.
Bonjour merci de votre réponse
J’ai essayé une nouvelle fois voici mes recherches :
aire des quatre carrés réunis découpés = 4x2 et Surface rectangle =40*25=1000
Cherchons x dans 1000-4x2.
Je trouve x2 =250 donc x=15,8113883
Mais que veut dire x? Je suppose qu’il correspond à la différence entre le rectangle et l’aire de 4 carrés découpés..
Je le divise par 4 ce qui me donne 3,95284....=x= ‘l’aire d’un carré découpé’
Je sais que la formule de l’aire d’un carré est Aire= c*c donc 3,95284 = 1,98..*1,98..
1,98..~2
x=2
Donc x est variable sur [0;2]
Bon je pense que ce calcule est farfelu donc ne me disputez pas si c’est faux...
Si vous pouvez me donner un indice de ce qu’il faut calculer pour trouver x je vous remercie.
Dernière modification par Lachimiecphysique ; 15/12/2019 à 14h58.
J’ai fait aussi d’autres recherches dont je pense correct mais qui ne servent pas vraiment pour répondre à la question 1):
Tu te compliques la vie ( et sans réfléchir dirait gg0 )
maintenant quelle est la hauteur de la boite qu'on est en train de construire ?Envoyé par Lachimiecphysique
et le volume c'est bêtement base*hauteur.
quand à l'intervalle de x , là je suis décu, car la réponse est bien plus simple:
on ne peut replier un rectangle des deux cotés d'une valeur supérieure à sa moitié .... c'est un truc de gosse !
Gg0 disait :(message 2)Pour bien comprendre ce qui se passe, tu peux faire un modèle à l'échelle 1/2 : Tu découpes dans une feuille un rectangle de 20x12,5, tu lui enlèves des carrés dans le coins, tu plies suivant les pointillés, à 90°, et tu as la boite (pas fermée en haut).
Manifestement, tu veux écrire des calculs sans savoir ni penser. Et tu ne suis pas les conseils, sinon tu aurais fini depuis longtemps. Et tu n'écrirais pas ces absurdités !! Tu peux continuer longtemps ainsi sans &aucun intérêt pour toi. Quant à moi, j'arrête là, je ne perds pas mon temps avec ceux qui agissent bêtement.
D'accord merci quand même.
Bonne soirée
tu as toutes les infos pour finir ton exo ! alors fais le, et dis nous !!
Cdt
Non c'est pas bon. Il semble que tu n'aies pas visualisé correctement la boite.
la surface du fond de la boite ce n'est pas 40*25. Le fond c'est ABCD dont tu as déjà correctement calculé la surface.
Sa hauteur c'est x. Donc le volume c'est ...
Applique le conseil de gg0 : effectue vraiment l'exercice de construction, fais la découpe des 4 coins, et constitue la boîte. Ca va aider.
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
