determiner la periode d'une fonction sinusoidale

[illias28]

salut à tous,
pourriez vous s'il vous plait m'aider à déterminer la période T d'une tension sinusoïdale qui a la fonction suivante v(alpha)=5*sin(alpha).
alpha étant un angle en degrés et que je connais v(20)=2
Merci
-----

[ansset]

bjr,
un coefficient multiplicateur ne change pas la période d'une fct périodique quelconque..
( uniquement son amplitude )
donc la question revient à "quelle est la période de la fct sinus ?".
pas très compliqué.

[illias28]

Merci Ansset pour votre réponse ,mais je ne sais pas comment faire,mon objectif est restituer la forme de cette tension sinusoïdale en précisant sa période sa valeur max et sa valeur min.pour ces 2 dernières c'est claire(dans cet exemple c'est +5v et-5v) mais pour la période je ne sais pas comment faire.Si vous pouvez m'aider un peu plus je vous serais reconnaissant.

[gg0]

Bonjour Illias28.

Avec v(alpha)=5 sin(alpha), que alpha soit en radians ou en degrés, on ne trouve pas v(20)=2. On trouve 4,56 ou 3,47, mais pas 2. Donc il y a un problème dans ce que tu nous dis. Peux-tu reprendre au début en nous donnant l'énoncé ?

Cordialement.

[A voir en vidéo sur Futura]

[illias28]

Merci ggo pour votre aide.vous avez raison ,c'est une valeur que j'ai donné au hasard sans faire les calculs,je m'excuse pour ça. au fait 5*sin20=1.71
ce que je voudrais calculer c'est la période de ce signal en seconde.je sais qu'une période c'est 2pi. mais comment faire pour trouver T en seconde,sachant que je ne connais que l’équation de cette fonction(dans cet exemple 5*sin(alpha) )

[Gwinver]

Bonjour.
En supposant qu'il s'agisse d'un exercice, il faudrait rechercher l'expression de alpha. Est-ce une valeur, une fonction etc. ... ,

[ansset]

ce qui ferait gagner du temps serait d'avoir l'énoncé depuis le début, pas uniquement cette formule.

[gg0]

Effectivement, mon 3,47 est un autre calcul.
Si tu dis que 5 sin(20) = 1,71, c'est que tu calcules en degrés et que c'est en fait 5 sin(20°).
Mais alors, si alpha est en degrés, la période de sin (en degrés) n'est pas 2 pi.

Tant que tu resteras dans le flou sur ce qui se passe (qui est ce alpha, quel signal est véritablement en cause, ...) on ne pourra pas t'aider : On ne peut pas deviner ce que tu as en tête .

[illias28]

Merci Gwinver pour votre aide.
non ce n'est pas un exercice, d’ailleurs je ne suis ni élevé ni étudiant,j'ai 50 ans je suis électronicien hobbyiste mais pas un bon mathématicien.en fait alpha est un angle en degrés mais on peut le remplacer par wt dans l’équation si on veut( v(t) = vmax * sin(wt) ) ce que j'aimerais savoir c'est si on peut calculer la periode en seconde de ce signal ne connaissant que v(t) à un instant donné.

[Gwinver]

Bonjour.

Bienvenu dans les études personnelles.

Malheureusement, la connaissance de la seule amplitude à un instant donné ne permet pas de déterminer la fréquence. En fait, il y a une infinité de sinusoïde pouvant prendre une valeur donnée, donc une infinité de fréquences.
Par contre, la connaissance de plus d'informations pourrait peut-être permettre d'évaluer la fréquence.

[illias28]

Bonjour
merci beaucoup pour votre aide Gwinver,et si on connaissait la valeur de v à 2 instants t1 et t2 et qu'on connait le temps entre t2 et t1 serait il possible alors de calculer la periode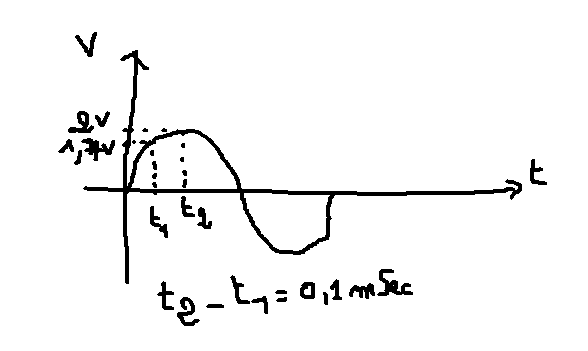

[gg0]

C'est un peu plus difficile que ça en général, car une fonction sinusoïdale a la forme f(t)=A sin(w t +phi). Donc la connaissance de deux valeurs à des moments t1 et t2 ne suffit pas à déterminer les trois constantes. Encore moins si on ne connaît même pas les valeurs t1 et t2, mais seulement l'intervalle entre.
Le problème de trouver la période d'un signal sinusoïdal est compliqué même si on montre qu'avec au moins 2 valeurs par période on peut théoriquement reconstituer le signal (2 valeurs par période sur un grand nombre de périodes). En pratique, il en faut plus, et avec une bonne précision.

Cordialement.

[Gwinver]

Bonsoir.

Le graphique donne l'impression que c'est possible. Mais, ce dessin présuppose que la période du signal est grande devant l'écart entre les deux points, c'est à dire que les points appartiennent à la même arche de la sinusoïde, et que l'un des points est la crête de la sinusoïde.
Cela étant dit, s'il s'agit de mesures, la précision est probablement moyenne.

[jacknicklaus]

Peut-être que vous ne dites pas tout. Dans votre dessin, il semble que le t2 soit au maximum de l'amplitude, donc t2 = 90°. ET vous connaissez une valeur de la fonction à t1, en connaissant seulement t2-t1.
Si ceci est correct, alors vous pouvez simplifier en considérant que votre fonction est f(t) = Asin(wt) où w est la pulsation. vous avez donc (angles en degrés)

1) fonction max = 2 V, donc A = 2.


2) f(t1) = 1.7 V, soit 1.7 = 2sin(wt1) = 2sin(90 - wD) où je note D = 90 - t1 = 0.1 msec
90° - wD = Arcsin(1.7/2) = 58.2° (en supposant le dessin correct : t1 entre 0 et 90)
wD = 32.8°
or D = 0.1 msec
donc w = 328°/msec
donc période = 360/w = 1.09 msec.

[illias28]

Merci beaucoup pour votre aide jacknicklaus ;j'ai remarqué que vous avez écrit 1.7=2sin(90-wD) au lieu de 1.7=2sin(90w - wD) est ce que vous avez utilisé une formule trigonométrique pour simplifier.

[jacknicklaus]

vous avez écrit 1.7=2sin(90-wD) au lieu de 1.7=2sin(90w - wD)

attention, sin(90w - wD) serait faux.

Gardez à l'esprit qu'un sinus consomme en entrée un angle. Exprimé en radians (usage en maths), ou en degrés voire en grades. Mais dans ces 3 cas, la valeur d'entrée est sans dimension : ne pas oublier qu'un angle est un rapport entre 2 longueurs.

sin(90 - wD) est dimensionnellement correct : 90 est un angle (sans dimension) correspondant à la valeur où le sinus = 1, w est la pulsation en angle/s (dimension [T^-1]), D est un temps (dimension [T]), donc wD est aussi sans dimension, et représente l'angle dont on a tourné pendant le temps D msec.

en revanche sin(90w - wd) est sans signification. 90 est sans dimension, w est de dimension [T^-1], donc 90w est de dimension [T^-1], et en prendre le sinus n'a aucune signification.