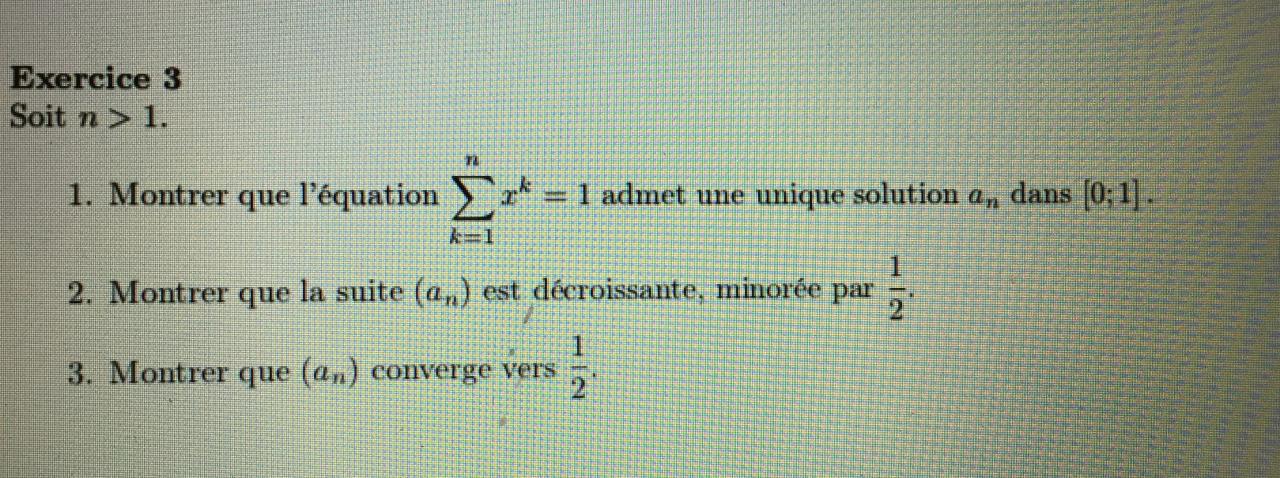Étude d’une suite convergente dont le terme général est solution d’une équation

[Marmus1021]

Bonjour !
Je bloque sur la troisième question d’un exercice.

J’ai appelé f_n la fonction qui associe à x la somme écrite dans l’énoncé de la question 1. J’ai réussi la 1 (avec le théorème des valeurs intermédiaires) et la 2 (en étudiant f_n+1 (a_n) et f_n+1(a_n+1) et en les comparant, sachant que f_n est strictement croissante).


En fait j’ai l’impression que je manque de méthodes pour prouver qu’une suite converge vers un réel a. Les seules que je connais, c’est par le théorème des gendarmes, et sinon résoudre a = f(a) quand on a une suite de la forme u_n+1 = f(u_n)

Donc voilà je veux bien que vous m’aidiez à résoudre la question 3 svp, et si vous avez d’autres méthodes pour déterminer qu’une suite converge vers un nombre a, je suis preneur : j’irai les étudier
Merci d’avance !
-----

[gg0]

Bonjour.

En écrivant la somme, pour x différent de 1 (1 n'est pas solution si n>1) sous forme d'un quotient, tu peux réécrire l'équation sous la forme


Tu as montré qu'il y avait une seule solution s(n) entre 0 et 1, que s(n)>1/2 et que la suite s(n) décroit. Pour montrer que 1/2 est la limite, il te suffira de démontrer que quel que soit a>1/2, tu peux trouver n de façon que s(n)<a. C'est simplement, dans ce cas particulier de suite décroissante minorée, une application de la définition de la limite. Tu la retrouves en posant
Pour ce faire, utilise l'idée que pour n grand, est très petit (puisque c'est une grande puissance d'un nombre inférieur à 1). Intuitivement, c'est négligeable et l'équation est en gros . Il reste à mathématiser ça, en justifiant par exemple que l'on peut choisir n de façon que .

Cordialement.

[Marmus1021]

Bonsoir ! J'ai essayé de rédiger mais je ne suis pas sûr d'avoir tout compris...
Soit ε >0. Posons a = 1/2 + ε. Choisissons n suffisamment grand pour que xⁿ⁺¹ < ε.
Alors on a ε-2x+1 >0, soit x < (1+ε)/2 < 1/2 + ε.
Donc x < a.
Ainsi, pour tout a > 1/2, il existe un n tel que s(n) < a. Comme s(n) > 1/2, on en déduit que la limite de cette suite est 1/2.

[gg0]

"Choisissons n suffisamment grand pour que xⁿ⁺¹ < ε." ??? C'est qui x ? Et il faudrait justifier que, pour le x que tu auras choisi, on peut bien trouver ce n.
Attention, on ne peut pas prendre pour x la solution d'une équation x^(n+1)-2x+1=0, puisqu'il faudra choisir n ensuite. D'ailleurs, tu ne démontres même pas que cette équation est utile.
Pour l'instant, tu n'as fait que paraphraser mon explication, sans démontrer.

Au travail !!

[A voir en vidéo sur Futura]

[Marmus1021]

Bon ça me paraît trop compliqué alors. J'ai cherché deux heures ce matin sans comprendre pourquoi ça ne marchait pas... C'est pas grave je vais faire tous les autres exercices, je laisse celui-ci de côté pour l'instant.

[gg0]

Je détaille un peu plus : déjà pour n=2, la solution a₂ est inférieure à 0,7. Donc si a_n est une solution, tu sais que an<0,7, donc
Tu peux déjà trouver un n (*) tel que l'on ait ce qui te permettra de reprendre ton explication sur de bonnes bases.
Rappel : par définition, a_n est le seul nombre entre 0 et 1 tel que


Cordialement.

(*) c'est un travail à faire. Dire "on peut trouver" ou "Choisissons n suffisamment grand pour que xⁿ⁺¹ < ε" n'est pas une preuve !!