Bonjour
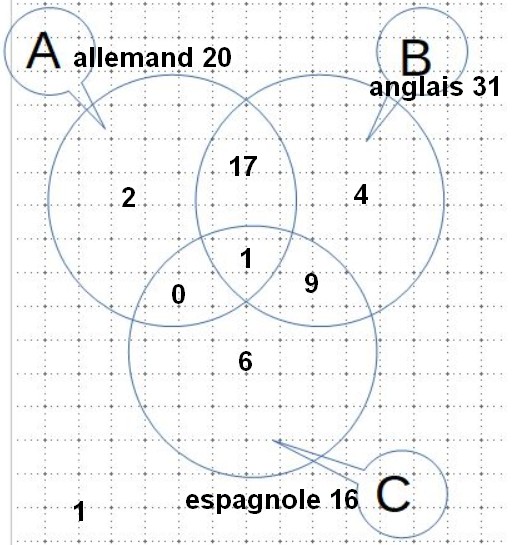
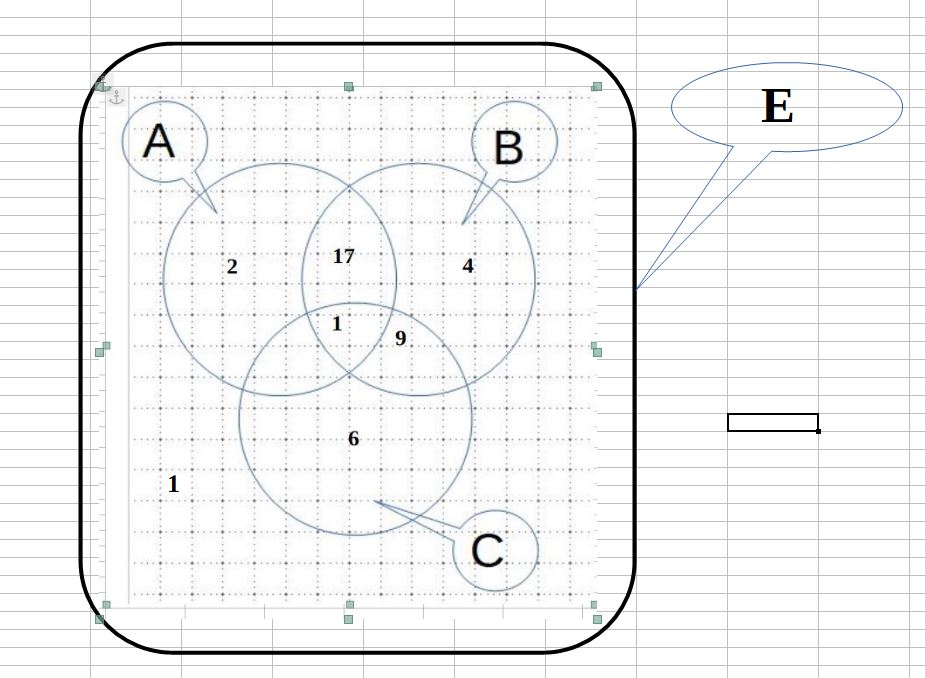
Dans une classe de 40 élèves, 20 étudient l'allemand, 31 l'anglais et 16 l'espagnol. 18 étudient l'anglais et l'allemand et parmi eux, 1 élève étudie aussi l'espagnol. Aucun n'élève n'étudie l'allemand et l'espagnol sans étudier l'anglais et seulement 6 élèves n'étudient que l'espagnol.
Je ne comprends pas du tout cette phrase !Aucun n'élève n'étudie l'allemand et l'espagnol sans étudier l'anglais
Merci d'avance.
-----



 est l'ensemble des élèves qui étudient l'allemand,
est l'ensemble des élèves qui étudient l'allemand,