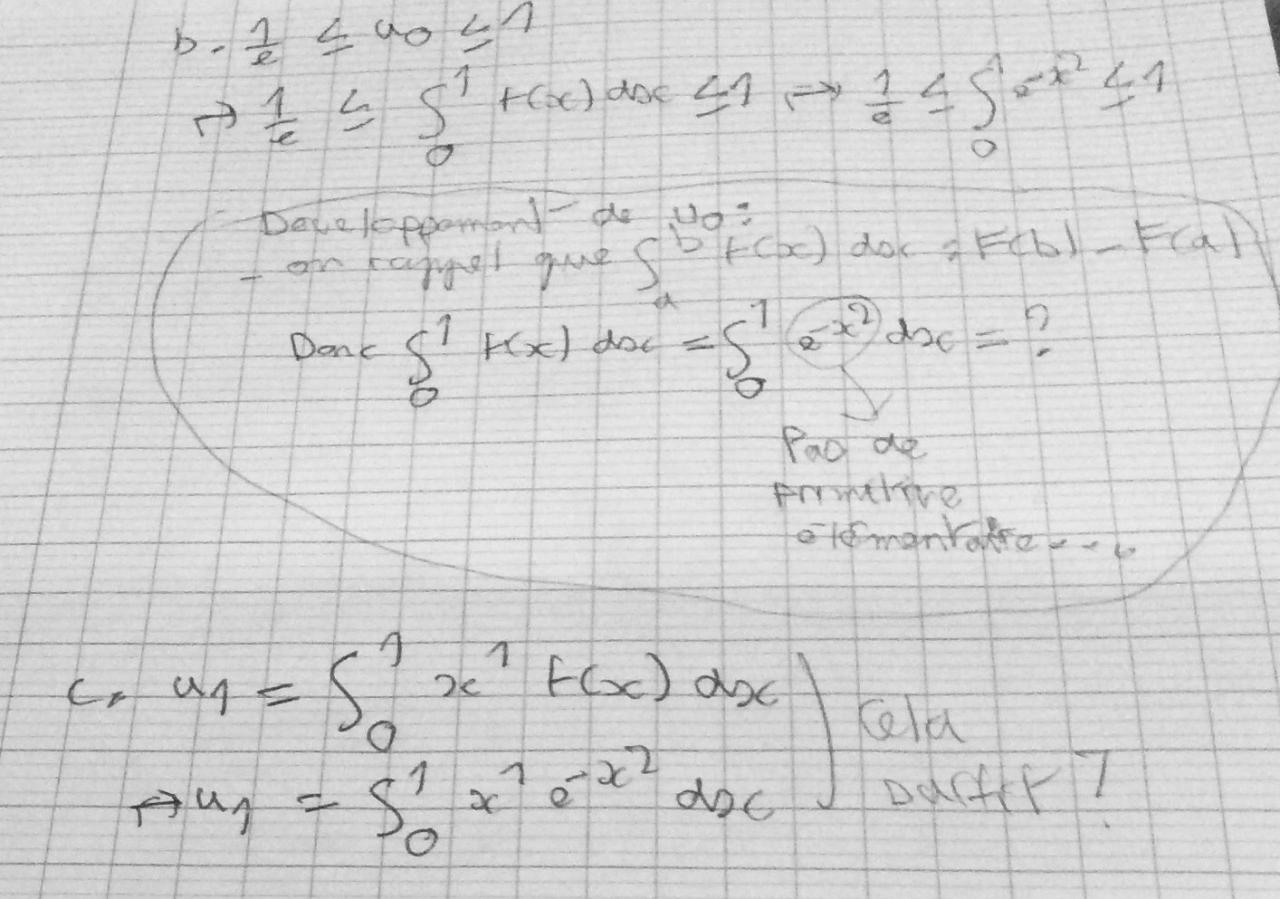Intégrales et suites

[Lachimiecphysique]

Bonsoir j’ai besoin de votre aide pour l’exercice suivant. Nous avons la fonction f définie sur l’intervalle [0;1] par f(x)= e^{-x^2}et on définit la suite (u_n) par :
Pièce jointe 439489

a) Démontrer que pour tout réel x de l’intervalle [0;1], 1/e <= f(x) <= 1.

b) En déduire que 1/e <= u₀<= 1

c) Calculer u₁

d) Démontrer que pour tout entier naturel n, 0 <= u_n.

e) Étudier les variations de la suite (u_n)

f) En déduire que la suite (u_n) est convergente.

g) Démontrer que, pour tout entier naturel n, u_n <= 1/n+1

h) En déduire la limite de la suite (u_n)

Mes réponses

a) Faut-il montrer ici par récurrence ?

J’ai fais ceci pour l’instant mais je sais que cela suffit pas :

1/e <=f(x)<=1
<—> 1/e <= e^{-x^2}<= 1






Merci pour votre aide, bonne soirée .
-----

[gg0]

Bonjour.

On ne peut pas lire ta pièce jointe (mauvais format ? Trop grosse ?), donc difficile de suivre ce que tu as écrit sur ce brouillon.
Donc il te faut redonner l'énoncé sous une forme lisible.
Pour la question a), d'où peut venir cette idée de récurrence ? Une récurrence sur quoi ? Les seuls entiers sont 0 et 1.
Pour ce que tu as fait, il faut une preuve. D'où sort la première ligne ? (la deuxième est la même !!)
Mais une fois cela démontré, la suite est évidente, si tu connais le cours et la formule qui parle d'intégrale et d'inégalité. Avec la définition actuelle de l'intégrale, c'est même intuitivement évident.

Pour la suite, si j'ai bien compris, tu as à intégrer x exp(-x^2), qui est (à un coefficient multiplicatif près) une dérivée simple. Voir dans ton cours, les formules élémentaires de calcul de primitives. Par contre, ce que tu as écrit, c'est seulement que la valeur de u1 est .. u1. Ce n'est pas faux, mais...

Tu perds beaucoup de temps à écrire une fois avec f(x), une deuxième avec exp(-x²), c'est une erreur de croire que "comme c'est plus long, j'en ai fait plus". Et quand il n'y a que ça, c'est la preuve évidente du fait que tu n'as rien fait !!

Cordialement.

[Lachimiecphysique]

Bonjour, merci pour vos réponses, je m’excuse pour l’énoncé.
Voici ce que j’ai fais pour l’instant, je vous souhaite bon courage et bonne journée.

A0762774-D8CA-4A17-A1C6-FD6B08D2C57F.jpg. (énoncé)

4459CA2C-B1F7-42B9-8F33-69C59DAE0D1D.jpg

35027C6C-804F-487B-98B8-499BA3FAC945.jpg

860BF4A9-A67D-4666-9750-F3AC08C6ED78.jpg

[Bastien83160]

Holà ! Regarde ce petit récap sur ce sujet ! Plutôt bien expliqué et détaillé ! Bon visionnage, j'espère que ca t'aidera
https://www.youtube.com/watch?v=P57Kgv1JdGo

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

je n'avais pas eu le temps d'y revenir. Quelques remarques :
a) tu ne démontres pas que f(x) est entre 1/e et 1. Elle y prend des valeurs, comme tu l'expliques, mais elle pourrait devenir nettement plus grande, ou beaucoup plus petite (*). Manifestement, tu n'as même pas étudié la fonction, même pas tracé sa courbe pour voir !! Un peu de sérieux ne te ferait pas de mal, c'est une application des cours de première.
b) Pas de chance, il n'y a pas de primitive de f qui s'écrit avec les fonctions que tu connais. Par contre, en utilisant le a) et les propriétés des intégrales lorsque f(x)<g(x), tu arrives directement au résultat. Cette technique se dit "intégrer l'inégalité". Et je te l'avais déjà dit.
c) la méthode est bonne, mais le calcul est faux parce que tu ne fais pas attention.
Je n'ai pas compris la dernière ligne de ton dernier document. Tu ne fais pas beaucoup d'efforts pour te faire aider !!

Au travail !


(*) Par exemple, si f(x)=x²+5x -6 pour x compris entre 0 et 1, f(0) = -6, f(1)=0, mais -6<=f(x)<=0 est totalement faux. Par exemple f(2) = 8.

[Lachimiecphysique]

Bonjour, merci pour votre aide (et pour la vidéo). Voici ce que j’ai fais pour l’instant, merci d’avance pour votre intervention et bonne journée .

A84765BE-127A-4680-85D0-7EDBFB5B0D35.jpg

EA3C031B-DA9A-4222-B31E-C6607D59006F.jpg

[gg0]

OK pour le b), mais toujours pas de vraie raison donnée pour le a). A quoi sert le calcul de la dérivée ?
Le c) démarre bizarrement ! C'est quoi ce N en exposant de x ? Il serait bien aussi de terminer le calcul.
Pour le d), l'idée semble être la bonne, mais c'est trop mal écrit, je ne lis pas tout. Il me semble qu'on peut rédiger ça en deux lignes.
Enfin dans le e) on ne te demande pas d'étudier "les variations d'une intégrale", mais le sens de variation d'une suite. Donc tu fais comme d'habitude ...

Cordialement.