Chemins Hamiltoniens - Spirale("s") d'Ulam ?

[Liet Kynes]

Bonjour,

Est-ce que l'on peut considérer que la spirale d'Ulam est un chemin Hamiltonien pour lequel les nombres impaires serait les sommets et les nombres pairs les arrêtes?

J'ai lu que si on prends pour premier nombre, dans la spirale d'Ulam, un autre nombre impair que 1 les propiétés d'llignements des nombres premiers restent semblables, serit-il juste de parler de chemin Hamiltonien avec des quadrillages finis qui se superposent ?

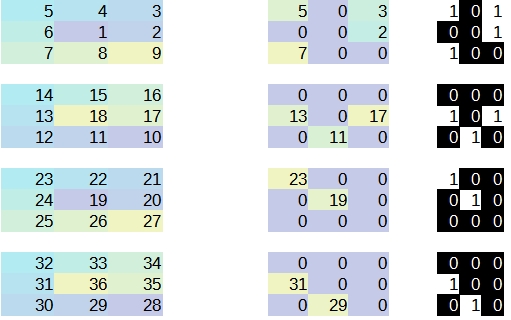
Par exemple en prenant un quadrillage à 27 sommets, une spirale qui tourne alternativement de l'intérieur vers l'extérieur et vis et versa (avec la possibilité de donner une règle récurente à la direction prise lorsque le changement de plans se fait au centre) :


-----

[Liet Kynes]

Petite boulette dans la présentation, je numérote uniquement les sommets et pas les arrêtes (j'ai un talent pour mal présenter mes idées au départ).
Et l'exemple du premier post concerne un quadrillage avec 3*3 sommets.

hared.jpg

J'ai chercher à tracer une spirale (pas de type Ulam) selon des motifs dont le centre est une partie de ceux qui permettent de trace les chemins de 3*3. Dans ce tracage selon la règle qui donne les nombres impairs représentant les sommets et les pairs pour les arrêtes cela pose un problème de chiralité:

hared2.jpg

[gg0]

Que de grands mots pour une explication floue ! Arrête la fumette, réfléchis à ce que tu fais, puis rédiges en essayant de penser à ce que vont comprendre les autres.

[Liet Kynes]

Bonjour ce n’est pas toujours simple*: cela ressemble à de la fumette , cela en a surement le goût mais cela n'en est pas ), d'autant que certaines questions me viennent une fois arriver un peu loin dans ma réflexion.

Petite tentative de réponse (mais concentration un poil limite après une journée de boulot assez longue et chargée )

La question principale peut surement se résumer ainsi : à quoi correspondent les nombres de la spirale d'Ulam dans un quadrillage infini? dans un quadrillage fini?

J'ai pensé qu'ils pouvaient dénombrer (selon l'ordre donné pour la formation d'une spirale) les sommets (ou intersections) du quadrillage ou dénombrer les carrés formés par les arrêtes.

Tout cela inspiré par le post de Mediat sur l'hyper-souris dans l'hyper fromage aux chemins Hamiltoniens (que je n'avais lu que trop vite au départ) .. mon imagination faisant le reste j'ai exploré l'idée en me rappelant que j'avais lu que quel que soit le nombre de départ la structure d'une spirale d'Ulam donne des alignements semblables avec les nombres premiers..

J'ai un peu exploré d'autre spirales pouvant être un chemin hamiltonien en envisageant le plus petit chemin d'un quadrillage fini (de n*n sommets impairs pour pouvoir avoir un centre) pouvant se réitérer dans un espace en trois dimension mais de là le nombre de variantes intéressantes à envisager explose.

Donc retour quand même sur le questionnement ci-dessus avant d'aller plus loin car si je peux aisément supprimer les nombres pairs d'un chemin hamiltonien partant du centre d'un quadrillage c'est que je numérote les arrêtes et les sommets du chemin alternativement par un nombre pair et un impair.. rien de spécial à ce niveau.

Si je prends la structure d'ulam je me dis que je compte deux choses différentes (sommets et arrêtes) alors que dans un chemin hamiltonien je peux ne compter que les sommets: est-ce alors possible de dire que la spirale d'Ulam est comparable à un chemin Hamiltonien ?

[A voir en vidéo sur Futura]

[Liet Kynes]

Si je prends la structure d'ulam je me dis que je compte deux choses différentes (sommets et arrêtes) alors que dans un chemin hamiltonien je peux ne compter que les sommets: est-ce alors possible de dire que la spirale d'Ulam est comparable à un chemin Hamiltonien ?

Bon j'ai compris ma confusion.. on peut considérer la spirale d'Ulam comme un chemin Hamiltonien qui compte uniquement les sommets.

Ce qui m'interessait c'est de n'avoir que des nombres impairs pour le chemin du coup dessiner une structure comme la spirale d'Ulam mais avec que des nombres impairs; il faut déssiner un chemin qui compte les sommets (en commencant par un sur un sommet: tout les sommets seront impairs) et les arrêtes puis supprimer tout les nombres pairs; cela reviens à rendre adjacents les sommets.

Sur une telle structure comportant 3*3 sommets il est possible de passer en 3d. Le chemin du premier plan une fois achevé on passe au second en repartant sur le dernier nombre du premier plan +2 etc..
Il y a plusieurs manières de tracé un plan mais on peut choisir de faire jouer n tracés différents un grand nombre de fois et regarder la quantité de nombres premiers apparaissant dans chaque case.

Ce que j'ai fait:

Au premier plan j'ai:

a1 b1 c1
d1 e1 f1
g1 h1 i1

En choisissant de jouer les tracés premeir plan : a-d-g-h-e-b-c-f-i (soit a1=1,d1=3,g1=5..i1=17) puis second plan : i-h-g-d-e-f-c-b-a (soit i2=19 , h2=21..a2=35) puis troisème plan a-b-c-f-e-d-i-h-g puis quatrième plan i-f-c-b-e-h-g-d-a et retour au tracé du premier plan pour le cinquième. Cela donne les valeurs suivantes:

1 11 13
3 9 15
5 7 17

35 33 31
25 27 29
23 21 19

37 39 41
47 45 43
49 51 53

71 61 59
69 63 57
67 65 55

73 83 85
75 81 87
77 79 89

Pour chaque lettre j'obtiens donc un algorythme qui me donne une suite de nombres impairs plans après plans. La lettre "e" centrale n'est jamais utilisée comme premier point du tracé et ne donne donc que des valeurs de nombres composés. Les 8 autres lettres se répartissent donc les nombres premiers. Le résultat c'est qu'au n-ème plan le groupe de lettres a-c-g-i cumulent quasi autant de nombre premiers chacune tout comme le groupe b-d-f-h et et chaque lettre du groupe a-c-g-i obtient quasi le double de nombres premiers que les lettres du groupe b-d-f-h.

Pour illustrer si a,b,c,d,e,f,g,h étaient des joueurs de cartes et si e avait un paquet de cartes ayant pour valeur les nombres impairs, et que e distribuait les cartes aux autres en s'en donnant une à lui même selon la méthode décrite ci dessus: quelque soit le temps de distribution, e n'aurait aucune carte avec un nombre premier, a,c,g,i auraient autant de cartes avec des nombre premiers et b-d-f-h aussi mais deux fois moins que les joueurs du groupe a,c,g,i.

Il est évidement possible de calculer les algorythmes pour chaque lettres mais je ne savais pas qu'il était possible de répartir les nombres premiers ainsi.
Ci dessous les courbes d'évolution du nombre de nombres premiers pour chaque lettres jusqu'à n=1500 (1500ème plan):

abc.jpg

Le rapport de la somme de nombre de nombre premier entre les groupes a-c-g-i et b-d-f-h:

rapport.jpg

[Liet Kynes]

Bonjour,

c'est très con ce que j'ai fait une fois que s'est ramené à l'arithmétique mais bon , cela m'apprendra à être un poil moins rapide avant de poster, cela dit je vais tester les suites sur des intervalles de nombres premiers significativement plus grand (pour lesquels la moyennes des écarts est très supérieure aux écarts entre premiers lorsqeu l'on commence à 3 sur un intervalle réduit comme ce que j'ai fait).. cela n'aura pas grande signification quend même.
Cette idée d'utiliser un chemin Hamiltonien me plait bien mais me permet surtout de me rendre compte de ma difficulté à réduire une idée à un niveau aritmétique une idée en intégrant pleinement ce qui se passe.

En grattant un peu sur l'idée d'écarts pour comprendre entre autre pourquoi il y a deux fois plus de premiers pour tel algortime qu'un autre et en laissant de côté mes délires Hamitoniens, j'ai expérimenté l'idée d'additionner à chaque impair les nombres pairs à partir de 2 et de localiser ensuite les premiers (voir PJ), cela donne aussi des figures qui semblent arrangées (comme pour Ulam) au final cette spirale est-elle vraiment un concept étudié en maths car cela me semble juste une impression visuelle pas très exploitable
?