Bonjour à tous
Mes notions de trigo étant loin, quelqu'un pourrait m'aider ?
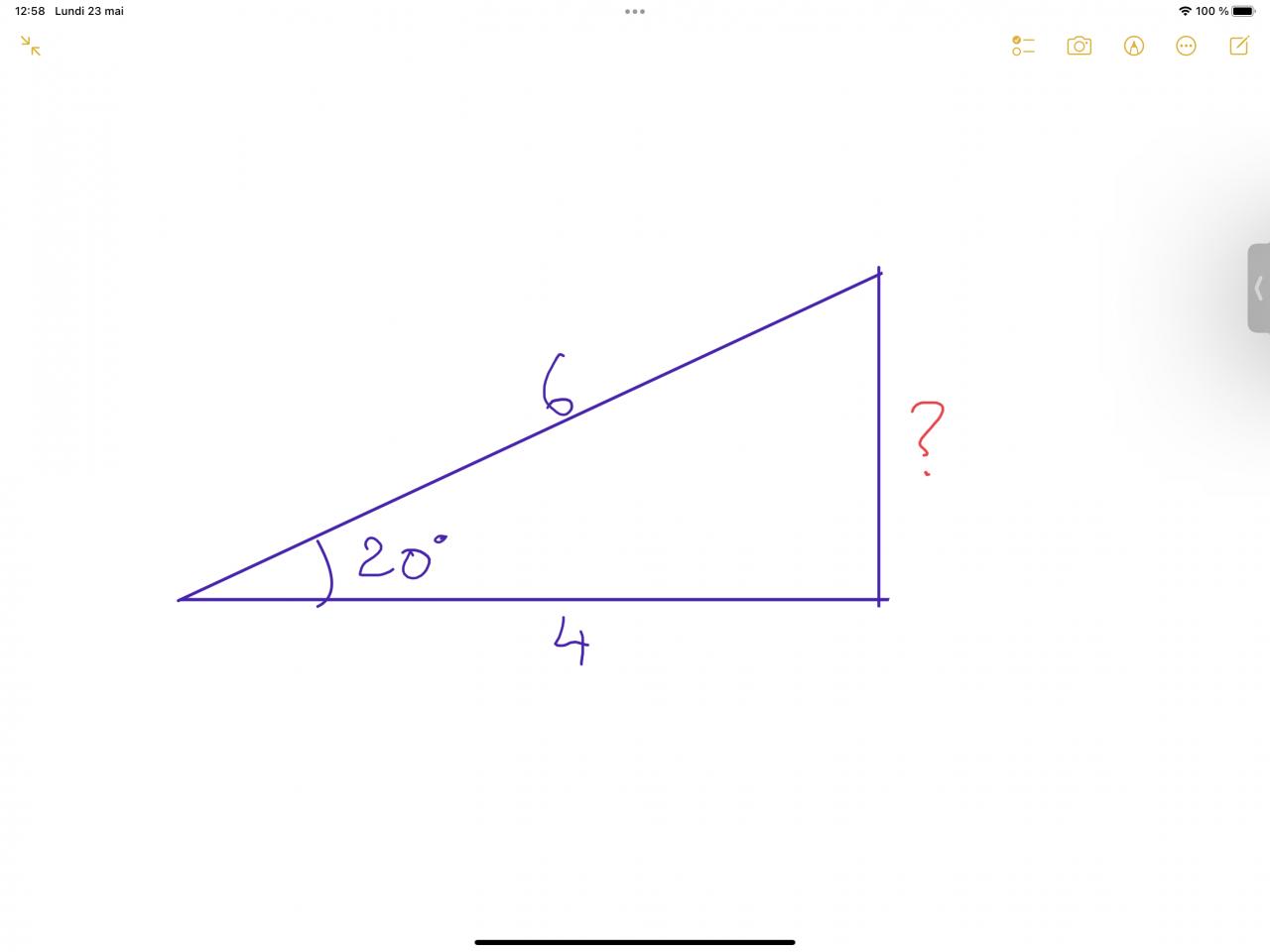
Sachant que j'ai la taille de 2 côtés d'un triangle
Et la mesure l'angle entre les 2.
Comment trouver la taille du 3° côté ?
Merci
-----

Bonjour à tous
Mes notions de trigo étant loin, quelqu'un pourrait m'aider ?
Sachant que j'ai la taille de 2 côtés d'un triangle
Et la mesure l'angle entre les 2.
Comment trouver la taille du 3° côté ?
Merci


Bonjour.
Tu peux utiliser la formule dite d'Al Kashi : BC²=AB²+AC²-2 AB AC cos(BAC).
Cordialement.

Euh, malgré le dessin joint, le problème est aussi qu'il ne s'agit pas d'un triangle rectangle
Dernière modification par Naos46 ; 23/05/2022 à 13h27.

Bonsoir !
Pour résoudre tes problèmes de trigo, un moyen mémotechnique suffit dans 90% des cas : CAHSOHTOA. Elle te permet de retrouver les formules de cosinus, sinus et tangente:
- CAH : Cosinus = Adjacent sur Hypoténuse ;
- SOH : Sinus = Opposé sur Hypoténuse ;
- TOA : Tangente = Opposé sur Adjacent.
Ici, l'utilisation de la trigo ne sers à rien, un théorème de pythagore suffit (tu es dans un triangle rectangle, et tu connais deux côtés). La trigo te servirait si tu n'avais qu'un seul côté, où si tu cherchais l'angle.
Bonne journée à toi !
(P-S : Je suppose ton triangle rectangle au vu du dessin, mais si ce n'est pas le cas il ne me semble pas que tu puisse utiliser la trigo non plus)
Dernière modification par Elenos2 ; 23/05/2022 à 13h30.

Attention Elenos, dans les deux cas de figure, il n'y a pas de triangle rectangle !!

J'ai ajouté un post depuis il ne s'agit pas d'un triangle rectangle !

Oups je n'avais pas vu
Je vais juste nommer les sommets afin de simplifier les explications: AB=6 , AC=3, BÂC=24° et on cherche BC
Ce que je vais faire là est juste une idée, aucune idée de si c'est juste ni si ça fonctionne:
Soit E le projeté orthogonal de A sur (BC). On a donc deux triangles rectangles en E : AEB et AEC, avec chacun deux côtés connus. On peut donc calculer BE et EC, et donc BC grâce à la relation de chasles.
Reste à trouver la longueur AE. J'ai pensé me situer dans un plan de vecteurs directeurs i(1;0) et j(0;1) passant par A, afin d'en faire émerger des coordonnées pour mes différents points, mais je n'ai pas réussi... Si quelqu'un voit comment creuser par là peut être?
(Edit: je n'avais pas vu que quelqu'un avait déjà donné une solutionje laisse quand même ma proposition, j'aimerais bien savoir si on peut trouver comme cela)
Dernière modification par Elenos2 ; 23/05/2022 à 17h46.

Eleno2 :
"Soit E le projeté orthogonal de A sur (BC). On a donc deux triangles rectangles en E : AEB et AEC, avec chacun deux côtés connus." ???
Dans AEB, seul AB est connu, et comme on n'a pas d'angle pour utiliser de la trigo élémentaire ...
Cordialement.

C'est justement le sens de ma question, existe-t'il un moyen de retrouver AE, je déduit de votre réponse que non

Merci pour vos solutions
Il y a aussi le théorème d'Al-Kashi :
BC ² = AB ² + AC ² -2 x AB x AC x cos A
Qu'en pensez-vous ?
C8749A50-87BD-4AA7-9FCC-8CD28368A360.jpg
Dernière modification par Naos46 ; 24/05/2022 à 01h58.

Bonjour Naos46. Lis-tu les réponses qu’on t’envoie ?
C’est exactement, mais avec une autre notation, la première réponse que gg0 t’a faite au post #2 !

Choom souligne 2 points importants : bien lire toutes les réponses, et pas qu'en diagonale (sauf pour les exercices sur les matrices), et ne pas être esclave des notations (savoir reconnaître une relation avec des notations différentes et/ou inhabituelles).
"Dans la vie, rien n'est à craindre, tout est à comprendre." Marie Curie


je ne comprends pas cette discussion qui tourne en rond, alors que le sujet est clos depuis la réponse #2..
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.

Mes excuses.Oups !
En effet ggo avait déjà répondu…Mes excuses.
A ce sujet j'ai appliqué ce théorème et il semble y avoir une erreur.
J'obtiens 2,4 alors que ce devrait être 4,8.
Sirius, 8,6 AL et Procyon, 11 AL
Angle : 25° 25' 00" (trouvé sur l'appli Starmap2)
Cos 25 : 1
Ci-dessous mon calcul :
BC ² = AB ² + AC ² -2 x AB x AC x cos A
BC ² = 8,6 ² + 11 ² - 2 x 8,6 x 11 x cos 25
BC ² = 8,6 ² + 11 ² - 2 x 8,6 x 11 x 1
BC ² = 73,96 + 121 - 189,2
BC ² = 5,76
BC = 2,4 au,lieu de 4,8
Où est l'erreur ?

bonjour,
le cosinus de 25° n'est pas 1 mais 0,91 et là on trouve 4,85.
JR
l'électronique c'est pas du vaudou!

Bonjour et merci
Comment trouves-tu ces résultats 0,91 et 4,85 ?
25 ° > 0,43 r
Cos (0,43 x 3,14/180) =0,44

Re
cos(25°) = 0,906308 calculette en degrés
de même
cos(25*PI/180) = 0,906308 calculette en radians
le reste coule de source!
JR
Dernière modification par jiherve ; 24/05/2022 à 13h27.
l'électronique c'est pas du vaudou!

J'ai lu dans les messages épinglés que nous n'étions pas sur un forum d'aide au devoirs mais de réflexion et d'échange. J'ai bien vu que vous aviez proposé une solution à ce problème, mais étant intéréssé par le sujet j'ai proposé une autre piste de réflexion, en demandant si il y avait un moyen de la compléter. Il me semble que le sens de ma proposition est tout à fait correct, puisque ma question est de savoir si l'on peut connaître AE. Je vous prierait donc de ne pas me manquer de rester courtois même si ce que je propose vous paraît stupide "sans sens" ou "peu sérieux". C'est peut être évident pour vous, mais ce n'est pas mon cas.Un peu de sérieux serait nécessaire.
Bonne soirée

Si tu veux être pris au sérieux, évite les affirmations fausses. Je rappelle : "Soit E le projeté orthogonal de A sur (BC). On a donc deux triangles rectangles en E : AEB et AEC, avec chacun deux côtés connus."
Ce n'est pas moi qui ai écrit cela, c'est toi. Alors que ça n'a aucun rapport avec la question posée.
Quels sont les deux côtés connus de AEB ?
Si tu es capable de le dire, je te fais 1000 excuses, mais en attendant, je continue à penser que je n'ai pas été discourtois, seulement factuel.

Il me semble que la phrase est assez claire. Je demande si vous connaissez un moyen pour retrouver AE. Nous sommes sur un forum pas dans une revue scientifique où l'on cherche à démontrer rigoureusement quelque chose. J'aborde ici une piste de réflexion, et je dis donc ce que je cherche à prouver, en demandant en dessous de l'aide sur la manière.Reste à trouver la longueur AE. J'ai pensé me situer dans un plan de vecteurs directeurs i(1;0) et j(0;1) passant par A, afin d'en faire émerger des coordonnées pour mes différents points, mais je n'ai pas réussi... Si quelqu'un voit comment creuser par là peut être?
Ce sera mon dernier message sur le sujet, inutile de polluer d'avantage cette discussion.
Bonne soirée

Bon, finalement, tu reconnais que le début de ton message était incorrect. Je n'ai pas parlé de la fin de ton message car il n'y a pas de réponse précise à ta question ; Soit on la pose seule et la réponse est oui (*), soit elle faisait suite à tes considérations précédentes et ça n'avait pas de sens.
Bonne soirée !
(*) il y a même des formules classique, même si on ne les voit plus maintenant : hauteur d'un triangle en fonction des éléments de ce triangle. Et c'était à la portée d'un élève de terminale à l'époque où j'y étais (et où on faisait beaucoup de géométrie).

