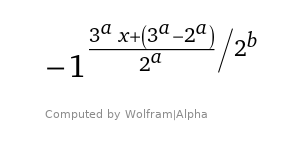La puissance judicieuse dans syracuse

[Liet Kynes]

Bonjour,

Je suis toujours dans mes recherches de trouver une solution à la phrase du doc Hal archives, https://hal.archives-ouvertes.fr/hal-01593181 , qui pose le problème de choisir une puissance de 2 judicieuse (fonction N(m) fin de la page 1 et début de la page 2).

Je suis passé à une fonction qui permet à partir d'un nombre impair de passer directement au prochain nombre impair sans avoir la suite croissante et décroissante, cela permet de n'utiliser qu'une seule formule donc je vais un peu au delà de la fonction N(m) décrite dans l'archive.

Exemple pour le nombre 11 on a classiquement ((11*3)+1)/2 = 17 -> ((17*3)+1)/2=26 -> 26/2=13

J'utilise donc la formule suivante pour un nombre impair x de départ: (3^a * x + (3^a - 2^a))/2^(a+b) avec la nécessité du choix judicieux de a et b
Pour 11 j'obtiens: ((3^2*11 + (3^2- 2^2))/2^2)/2^1=13

si l'on réitère sur le nombre suivant et le suivant.. il s'agit d'une fraction continue dont les termes s'annuleraient pour tout x pour obtenir une égalité entre dividende et diviseur tel que ceux-ci soient de la forme 2^n :c'est ce qui est conjecturé.

la fraction ici représentée pour 3 itérations (j'ai nommé les puissances a,b,c,d,e,f, en fonction de x certaines peuvent être égales entre elles):

MSP5861201cdb77b7fea0h600006ab79d63fb2chdh0.gif

Les nombres obtenus sont tous de la forme (6*n+(-1)^n-3)/2 (on en a parlé dans un autre post pour un sujet autre justement hier) bref exit les multiples de 3.

J'ai trouvé une équation intéressante pour tenter de trouver les valeurs de a et b dans la formule (3^a * x + (3^a - 2^a))/2^(a+b) :

Pièce jointe 460664

La question est connaissant x est-ce que je peux déduire a et b de cette équation?
-----

[Liet Kynes]

C'est bizarre, il y a une image qui apparait alors qu'elle ne devrait pas,

L'équation est bien celle-ci:

Pièce jointe 460664

[Liet Kynes]

Après simplification je trouve :

(((-1^((3^a x + (3^a - 2^a))/2^a/2^b) - 3)))=-4
(((-1^((3^a x + (3^a - 2^a))/2^a/2^b))))=-1
(((1^((3^a x + (3^a - 2^a))/2^a/2^b) )))=1



la contrainte étant que a et b sont >0

[Liet Kynes]

Bon ben j'ai trouvé la solution qui se résume en peu de mots : je suis pas malin

(-1^((((3^a*x)+(3^a-2^a))/2^a)/2^b)



-1 à la puissance d'un nombre impaire cela fait toujours -1



Le fil peut être clôturé

[A voir en vidéo sur Futura]

[Liet Kynes]

Pour la petite histoire, j'étais parti de la formule générant les nombres égales à 1 et 5 modulo 6
(6*n+(-1)^n-3)/2 permet donc, et c'est subtil (enfin pour moi), d'alterner -1 et 1 si n est pair ou impair.

[Brinicle]

Bonjour,

La question est connaissant x est-ce que je peux déduire a et b de cette équation

Avec une équation et deux inconnues ça paraissait déjà compliqué...

[Liet Kynes]

Bonjour,



Avec une équation et deux inconnues ça paraissait déjà compliqué...

J'ai quelques indications quand même:

C'est la relation entre les puissances dans la fraction continue avec un nombre impair x de départ qui m'intéresse.

MSP5861201cdb77b7fea0h600006ab79d63fb2chdh0.gif

La première étape de cette fraction continue est cette formule ou x,a et b sont des entiers >0 et x est impair:

MSP16131hec8g0979cbb8cf000042683f63051e761e.gif

Chaque fraction donne un nombre égale à 1 ou 5 modulo 6.

a=1 pour les nombres de la forme 12n+1 et 12n+5

La valeur b du prédécesseur d'un nombre 1mod6 est impaire et celui d'un nombre 5mod6 est paire.

Pour illustrer 55 égale 1 mod 6, avec les premiers nombres permettant d'obtenir 55 avec la formule, les valeurs de b sont impaires:

nombre de départ /a /b /nombre d'arrivée


73 / 1 / 1 / 55
195 / 2 / 3 / 55
293 / 1 / 3 / 55
1173 / 1 / 5 / 55
4693 / 1 / 7 / 55
8343 / 3 / 9 / 55
12515 / 2 / 9 / 55
18773 / 1 / 9 / 55
75093 / 1 / 11 / 55
300373 / 1 / 13 / 55