Syracuse

[Liet Kynes]

Bonjour,

Dans l'archive La suite de Syracuse, un monde de conjectures il est évoqué page 1 la suite N définie que pour les nombres impairs. Elle est donnée par la formule :
N(m) = 3m + 1/2p avec p judicieusement choisi.

Le truc c'est qu'il faut chercher p pour chaque nombre impair et que la "réduction" c'est à dire le nombre de terme reste longue.

En cherchant un peu (voir un peu plus ) j'ai trouvé cette formule plus efficace à réitérer en commencant par un nombre impaire:



Le choix "judicieux" concerne donc a et b pour obtenir un entier impaire mais cela représente moins de choix que la suite N citée dans l'article qui comprend bien plus de termes.

Sur Wolfram avec 1 comme résultat on retrouve bien le cycle trivial: https://www.wolframalpha.com/input?i...29%2F2%5Eb%3D1

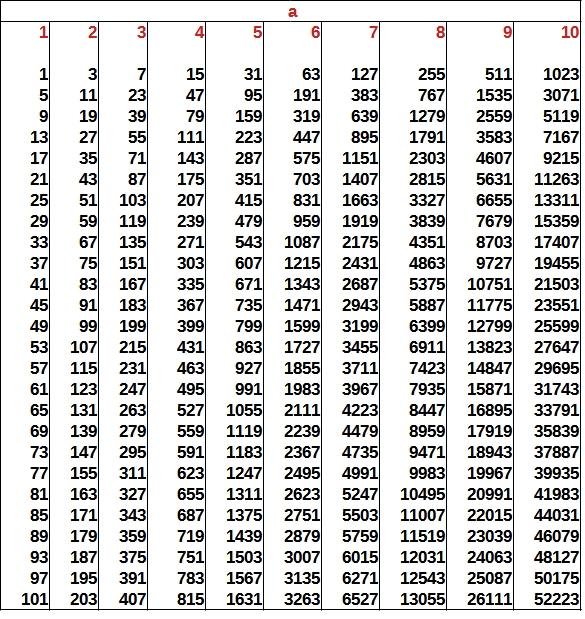
Pour les suites commencant par un impaire de 1 à 63 :

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
7 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
9 7 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1
11 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
13 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
15 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
17 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
19 11 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1
21 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
23 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
25 19 11 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1
27 31 121 91 103 175 445 167 283 319 911 577 433 325 61 23 5 1
29 11 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1
31 121 91 103 175 445 167 283 319 911 577 433 325 61 23 5 1 1
33 25 19 11 13 5 1 1 1 1 1 1 1 1 1 1 1 1
35 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
37 7 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1
39 67 19 11 13 5 1 1 1 1 1 1 1 1 1 1 1 1
41 31 121 91 103 175 445 167 283 319 911 577 433 325 61 23 5 1
43 49 37 7 13 5 1 1 1 1 1 1 1 1 1 1 1 1
45 17 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1
47 121 91 103 175 445 167 283 319 911 577 433 325 61 23 5 1 1
49 37 7 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1
51 29 11 13 5 1 1 1 1 1 1 1 1 1 1 1 1 1
53 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
55 47 121 91 103 175 445 167 283 319 911 577 433 325 61 23 5 1
57 43 49 37 7 13 5 1 1 1 1 1 1 1 1 1 1 1
59 67 19 11 13 5 1 1 1 1 1 1 1 1 1 1 1 1
61 23 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
63 91 103 175 445 167 283 319 911 577 433 325 61 23 5 1 1 1

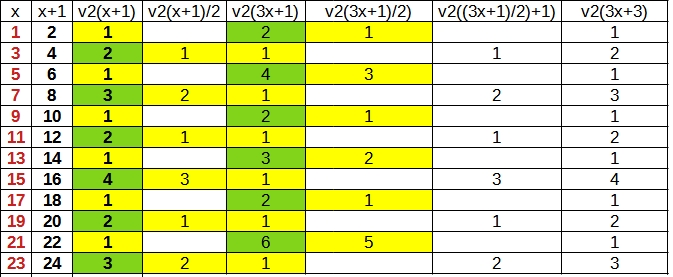
Ma question est comment montrer que pour x un nombre impaire il n'existe qu'un couple (a,b) tel que le résultat soit un nombre impair ?
-----

[Liet Kynes]

Bonjour, cela n'intéresse pas grand monde mon histoire, la formule brute que j'ai trouvé est (((3^a*x)+(3^a-2^a))/2^a)/2^b . Je reste toujours dans mon raisonnement de départ sur le système 3x+1/2.

J'ai construit la formule en prenant pour base la génération de nombres impairs par les nombres de Mercenne sur les n premiers termes avec l'algorithme de syracuse mais pas que.. et comme dit mon gamin, "le truc c'est que ton raisonnement est peut-être simple mais que tu es parti loin et que pour accrocher il faut des plombes avec ta façon d'exprimer les choses", et c'est pas faux.

Si quelqu'un veut décrypter, je met un .ods avec la construction.

Le raisonnement se base sur les nombres de type 3^a-2^a, a étant un entier quelconque. L'inspiration de la formule était dans le post suivant https://forums.futura-sciences.com/m...un-nombre.html mais j'ai fini par trouver ce que je propose ici pour réduire mon problème.

Dans la formule donnée dans ce fil la valeur de"a" pour chaque nombre impair de départ (pris dans l'ordre croissant de 1 à n+2) correspond à la suite A001511, pour b je cherche une formule mais à mon avis c'est sans espoir.

Pour l'idée développée dans ce fil, ce qui est intéressant c'est que l'on considère à une étape croissante puis décroissante et qu'il doit y avoir moyen de développer cela sous forme de formules qui donne des séquences croissantes/décroissantes/croissantes... j'ai croisé l'idée en chemin mais il faut que je retrouve la méthode (pas noté), c'est une histoire de fractions continues.

Bref, cela n'apporte pas grand chose à la résolution de la conjecture mais cela permet de la voir avec un oeil combinatoire, c'est un poil compliqué a expliquer mais les séquences étant de longueurs variables il faut envisager ce qui empèche l'existence d'un autre cycle dans ce sens (on retombe ou pas dessus).

Bon je mets ma pièce jointe pour ceux que cela interesserait, pour ceux qui savent que ce n'est pas interessant merci de l'indiquer à la communauté pour qu'ils ne perdent pas de temp dessus.

a b syr.ods

Pour ceux qui veulent tester le "choix judicieux" se fait simplment , il faut mettre le colonnes a et b avec 1 comme valeur, si le résultat (deuxième colonet si a=1 ,b=1 et le résultat est impair il n'y rien à faire.

[Liet Kynes]

Dans la formule donnée dans ce fil la valeur de"a" pour chaque nombre impair de départ (pris dans l'ordre croissant de 1 à n+2) correspond à la suite A001511, pour b je cherche une formule mais à mon avis c'est sans espoir.

Finalement non, on peut trouver, pas le temps de développer ce matin mais pour chaque x nombre de Mercenne on trouve une formule pour b.

[Médiat]

Ma question est comment montrer que pour x un nombre impaire il n'existe qu'un couple (a,b) tel que le résultat soit un nombre impair ?

Bonjour,

C'est faux, pour x = 7, (0, 0), (1, 0), (2, 0) et (3, 1) donnent des impairs. En étudiant la valuation 2-adique de 1 + x, on trouve cela très vite.

En choisissant le plus grand a l'unicité est garantie.

[A voir en vidéo sur Futura]

[Liet Kynes]

Bonjour,

merci pour cette réponse, je n'ai pas eu le temps de me pencher sur la valuation 2-adique de 1 + x, je ne connais pas bien cette notion.
Si je comprends bien, il faut présenter cette formule avec a>0 et si a>0 alors b>0 pour obtenir un impair ?

[gg0]

Tu n'as pas sérieusement lu la réponse de Médiat ! Évite les idées préconçues !!

[Liet Kynes]

Oui trop vite lu ce matin..

"En choisissant le plus grand a l'unicité est garantie."

C'est d'ailleurs comme cela que j'ai fait en commencant par incrémenter a puis b une fois que le résultat est pair. Je n'ai pas encore très bien saisi l'explication par la valuation 2-adique dont parle MEDIAT mais je découvre.

J'ai trouvé une introduction qui me semble correcte pour comprendre ( http://mathem-all.fr /bw/introductionanalysepadique.pdf )

"Définition 1.1 (Valuation p-adique). Soit p un nombre premier. On appelle valuation p-adique l’application vp : Q → Z ∪ {+∞} définie comme suit :
— vp(0) = +∞ ;
— si n est un entier non nul, vp(n) = k si p^k divise n et p^(k+1) ne divise pas n (p^k est la
« plus grande puissance de p dans n ») ;
— si n = a/b avec a et b des entiers non nuls, alors vp(n) = vp(a) − vp(b)."

Le cas de la la valuation 2-adique de 1 + x avec x impair permet d'utiliser la propriété vp(n) = vp(a) − vp(b) mais il faut que je trouve des exemples car j'ai du mal à comprendre avec la théorie pure.

J'ai regardé un peu mieux mon problème pour déterminer les valeurs de a et b et je me rend compte qu'il faut bien comprendre cette suite The ruler function: 2^a(n) divides 2n. Or, a(n) = 2-adic valuation of 2n. mais je ne dois pas me tromper si je dit que l'on ne peut pas calculer a à partir de x, ce que j'ai un instant cru dans mes messages précédents.

[Liet Kynes]

je ne dois pas me tromper si je dit que l'on ne peut pas calculer a à partir de x, ce que j'ai un instant cru dans mes messages précédents.

Bon si finalement, c'est assez facile!

[Liet Kynes]

Bonjour,

J'ai cherché mais pas trouvé (trouvé pleins d'autres choses mais pas celle là) , "The ruler function" c'est quelque chose d'assez scotchant, je suis resté la dedans depuis mon dernier post.
Comment expliquer qu'un nombre impaire fois 3 puis plus un et sur deux va rester impaire autant de fois que ce nombre plus un va être divisible par 2 ?

Le mot calcul de mon dernier post n'a pas de sens.

[Liet Kynes]

Ce que j'ai trouvé pour x un nombre impaire, c'est la relation v2[x+1]=v2[(x+1)/2]+1=v2[2x]-1

La formule étant (((3^a*x)+(3^a-2^a))/2^a)/2^b

(3/2)^v2[x+1]*(x+1)-1 = (((3^a*x)+(3^a-2^a))/2^a)

et

Si v2[x+1]=a , v2[(3/2)^v2[x+1]*(x+1)-1]= b = v2[(3/2^(v2[2x]-1)*(x+1)-1]

[gg0]

"v2[x+1]=v2[(x+1)/2]+1=v2[2x]-1" Faux.

x étant impair, v2(2x)=1, donc v2[2x]-1=0.

Et c'est de l'arithmétique très élémentaire !

[Liet Kynes]

Oui j'ai fait n'importe quoi.

J'en suis là mais je coince un peu:

v2[(x+1)] = v2[(3x+3)]

Si v2[(x+1)]=1 alors v2[(3x+1)] = v2[(3x+1)/2)] + 1

Si v2[(x+1)]>1 alors v2[(3x+1)]=1

Ensuite je ne trouve pas comment avancer.

[Liet Kynes]

Bonjour,

je sèche complètement sur ce problème, j'ai trouvé quelques relations à l'intèrieur de la suite http://oeis.org/A001511 mais sans plus.

Montrer que en partant de x (x étant impaire) le résultat reste impaire jusqu'à un nombre paire autant de fois que x+1 est divisible par 2, c'est à dire autant de fois que la valeur de (v2(x+1))

ex: pour x=7

(3*7+1)/2=11, (3*11+1)/2=17 et (3*17+1)/2=26 donc 11,17,26
v2(x+1)= v2(7+1) = 3


Il me semble que la démonstration avaité été donnée sur le forum (par Mediat peut-être?) si quelqu'un a gardé se souvenir, je suis preneur.

Merci

[Liet Kynes]

Rien de plus, un mois là-dessus sans progrès. Je dois être comme celui qui cherche l'eau dans le verre en regardant que sa paroi.
j'ai trouvé que pour b dans la formule que je propose, il est possible de tendre vers la symétrie obtenue avec a, mais je ne trouve pas pourquoi, je pense qu'il y a un lien avec ma question initiale.

Pour b, b de x+2^k tend à être égal à b de x(assez rapidement d'ailleurs).
Pour a la symétrie est parfaite entre deux nombres de Mercenne.
La formule peux s'écrire plus simplement avec avec c=a+b