Exercice de math sur les probabilité

[mln1725]

Bonsoir, j'ai un exercice de math à faire pour la rentrée, mais malheureusement je suis bloquée.

voici l'énoncé :
Une entreprise fabrique des cartes mères. La proportion de carte défectueuses produites est p, avec 0 ≤p ≤ 1. Le directeur met en place un système de test systéma- tique pour éviter de mettre sur le marché des cartes défectueuses. Pour des raisons techniques, ce test n'est pas parfait. Il exclut de la mise sur le marché seulement 95 % des cartes défectueuses mais aussi 2 % des cartes non défectueuses

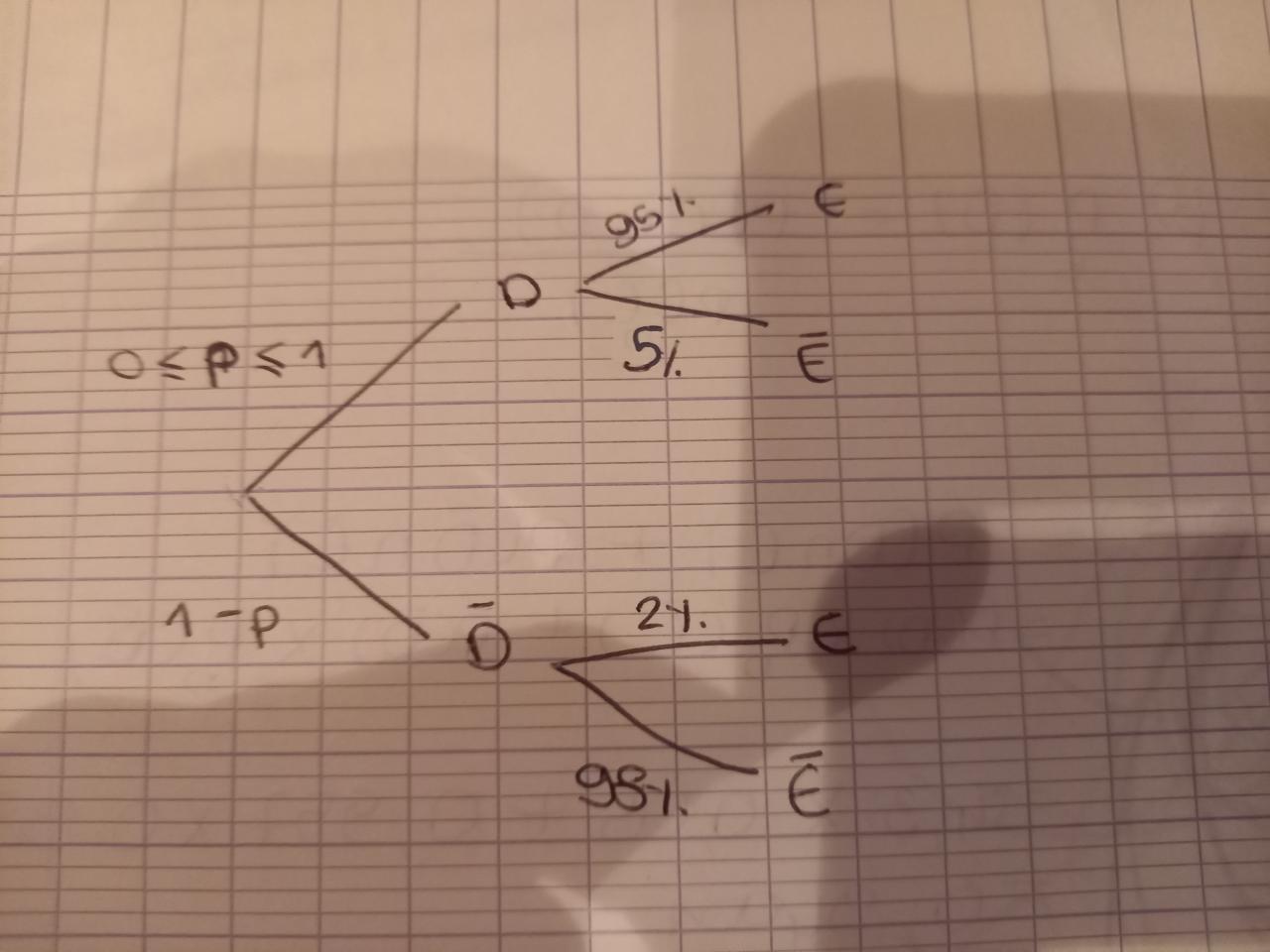
1. Compléter l'arbre de probabilité ci-dessous. On note D l'évènement « La carte est défectueuse >> et E l'évènement « La carte est exclue de la mise sur le marché »>
2. Le directeur constate que 6 % des cartes fabriquées
sont exclues de la mise sur le marché.
a. Calculer la valeur de p. Arrondir au 10puissance -4.
b. Calculer la probabilité qu'une carte soit défectueuse sachant qu'elle a été mise sur le marché. Arrondir au millième.
3. Le directeur souhaite que la probabilité qu'une carte soit défectueuse sachant qu'elle a été mise sur le marché soit désormais inférieure ou égale à 0,1 %. Pour cela, il veut améliorer la qualité de fabrication et ainsi diminuer la proportion p de cartes produites défec-
tueuses, tout en conservant le même système de test. Déterminer les valeurs de p pour que son objectif soit
atteint.

mon travail :
1;

arbre pondéré


2. je penses que je 6% correspond à P(E) mais je ne suis pas sur.
donc :
P(E)= P(DinterE)+P(D(barre)interE)
=P(D)xP(E)sachant D+P(Dbarre)x P(E) sachant Dbarre
=px0,95+(1-p)X0,02
0.06 =0,95p+0,02p+0,02

p est donc égal à 0,043 ??

3. on cherche P(D) sachant E barre

= P(Ebarre inter D)/P(Ebarre)

on calcul P(Ebarre) = (je ne détaille pas mais jai trouvé ) = 0,94001

ensuite on calcul P(D) sachant E barre = 0,957x 0,98 / 0,94001 = 0,99... ( ce qui me parait faux)

merci d'avance
-----

[gg0]

Bonjour.

La démarche est bonne mais je ne trouve pas comme toi pour p. Je trouve plutôt 0.0412 (0.04/0.97).
Pour la suite, le 0.98 n'a rien à faire là, il concerne Dbarre.

Cordialement.

[mln1725]

Pour le résultat de p j'ai mal recopier le résultat de p :
0.06= 0.95p+0.02-0.02p ( lorsque on develope (1-p)×0.002 il y a bien un moin qui reste)

Pour la suite il me semble avoir rectifier j'ai trouvé que

P(D) sachant Ebarre = P( Ebarre inter D) / P(Ebarre)

On connaît P(E) = 0.06 on peu donc déterminer p(Ebarre) = 0.94.

P(D) sachant Ebarre = P(D)× P(Ebarre) sachant D / P(Ebarre)

0.043×0.05/0.94 = 0.002 = 0.2%

3. On remplace p(Ebarre) par 0.001 pour connaître la valeur de p à modifier

Actuellement le p est à 0.043, et il faudrait qu'il soit à 0.02

[gg0]

OK pour le 0,43.
Pour le reste, je ne suis pas dans les conditions d'un calcul sérieux.

A +

[A voir en vidéo sur Futura]