Aire et volume d’une sphère avec son diamètre

[EspritTordu]

Bonjour,

Le volume d’une boule est défini avec son rayon R, Vr=4/3*pi*R^3 (eq.1), son aire vaut Ar=4*pi*R^2 (eq. 2) et est la dérivée de (1) selon R.

Maintenant je considère le diamètre D comme paramètre plutôt que son rayon R de façon que R=D/2 : cela donne (tout compte fait) :
depuis (1) Vd=pi/6*D^3 (eq. 3)
depuis (2) Ad=pi*D^2 (eq.4)

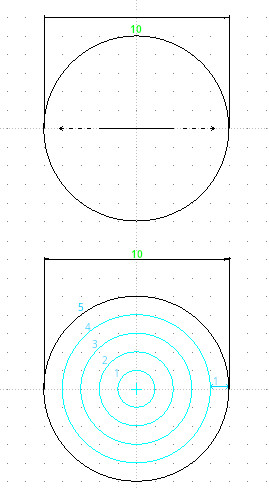
Je me propose d’intégrer (4) pour retrouver le volume, en considérant qu’une boule est la somme infinie d’une aire de sphère de 0 à D :
Vd2=pi/3*D^3 (eq. 5) .... soit deux fois trop que la référence (3) ?

De même, si je dérive (1) pour chercher l’aire d’une sphère :
Ad2=pi/2*D^2 .... soit deux fois moins que la référence (2) ?

Quelle logique conduit à avoir une différence de 2 soit en trop ou en moins ? Pourquoi je calcule deux fois la même chose d’un côté semble-t-il, et de l’autre je ne fais que la moitié ?

Merci d’avance.
-----

[Resartus]

Bonjour,
Quand vous intégrez la surface pour obtenir le volume, c'est par couches successives à partir du centre. La variable d'intégration part de 0 et va jusqu'à R, pas jusqu'à D....

[EspritTordu]

De même, si je dérive (1) pour chercher l’aire d’une sphère :
Ad2=pi/2*D^2 .... soit deux fois moins que la référence (2) ?

C’est une erreur, veuillez comprendre que l’on dérive depuis l’équation 3, Vd=pi/6*D^3 (eq. 3)

[EspritTordu]

Quand vous intégrez la surface pour obtenir le volume, c'est par couches successives à partir du centre. La variable d'intégration part de 0 et va jusqu'à R, pas jusqu'à D....

...Pourriez-vous s’il vous plaît développer ? Qu’en est-il de la dérivée Vd=pi/6*D^3 (eq. 3) => Ad2=pi/2*D^2 (eq. 6)

[A voir en vidéo sur Futura]

[Resartus]

Re,
C'est votre phrase ci-dessous qui est fausse :
"en considérant qu’une boule est la somme infinie d’une aire de sphère de 0 à D"

La somme des aires successives de sphères ne va pas de 0 jusqu'à D, mais seulement de 0 jusqu'à D/2, puisque on part du centre...

[MissJenny]

annulé : j'avions mal compris

[EspritTordu]

Re,
C'est votre phrase ci-dessous qui est fausse :
"en considérant qu’une boule est la somme infinie d’une aire de sphère de 0 à D"

La somme des aires successives de sphères ne va pas de 0 jusqu'à D, mais seulement de 0 jusqu'à D/2, puisque on part du centre...

1-Mais si j’intègre alors (eq.4) pi*D^2=> [pi/3*x³]-[pi/3*0³] => avec d/2 : pi/(3+8)*d³ ????

2-Quant à la dérivée de (eq.3) Vd=pi/6*D^3, il n’y a pas de paramètre à faire varier?

[Resartus]

Bonjour,
Dans ce calcul le volume s'obtient à partir de l'aire, en intégrant par dR, et de même, c'est la dérivée du volume par rapport à R qui donne l'aire.
Vous pouvez choisir d'exprimer le volume en fonction de D, mais dans ce cas, il faut multiplier par la dérivée de D par rapport à R (ici 2) pour calculer la dérivée

Plus généralement (je suppose que vous connaissez la notation en "d" pour les dérivées) pour toute fonction f(y(x)), on a df/dx=df/dy*dy/dx

Et réciproquement, quand on intègre, il faut diviser par la dérivée de D par rapport à R

[gg0]

Bonjour EspritTordu.

Il y a une raison forte au fait qu'en dérivant la formule du volume d'une sphère en fonction de son rayon (f(R)=4/3 pi R^3) on obtient l'aire extérieure (f'(R)=4 Pi R²). Elle apparaît dans la démonstration de la formule du volume par "couches successives". La variable qui fonctionne, c'est R. Vouloir reproduire ces calculs avec une autre variable ne peut aboutir.
Finalement, c'est ce que tu as trouvé, et il te faut l'admettre. Les maths sont dures, mais c'est les maths.

Cordialement.

[EspritTordu]

Bonjour,
Dans ce calcul le volume s'obtient à partir de l'aire, en intégrant par dR, et de même, c'est la dérivée du volume par rapport à R qui donne l'aire.
Vous pouvez choisir d'exprimer le volume en fonction de D, mais dans ce cas, il faut multiplier par la dérivée de D par rapport à R (ici 2) pour calculer la dérivée

Plus généralement (je suppose que vous connaissez la notation en "d" pour les dérivées) pour toute fonction f(y(x)), on a df/dx=df/dy*dy/dx

Et réciproquement, quand on intègre, il faut diviser par la dérivée de D par rapport à R

Si je dois mettre en phrase cela :
« Ma variable d’intégration est implicite, c’est R, et j’affiche le résultat avec D. Je dois donc savoir comment D évolue par rapport à R pour faire la somme » , C’est une imbrication de paramètres, donc ?


(corrigez-moi si je me trompe) :

Pour la dérivée du volume [1] pi/6*D^3 :
=>D=2R => dérivée selon R c’est 2, pour chaque différentiel dD élémentaire, j’ai en fait dD=2dR
=>on corrige alors pour chaque élément de dérivée (chaque couche successive) : on corrige [6] par ce facteur de façon que [6] Ad2=pi/2*D^2 × 2 => donne la bonne référence [3] Ad=pi/2*D^2 !


Pour l’intégration de l’aire [4] pi*D^2 :
=> l’intégration (et surtout les formules de primitives) ne sont capable que de sommer des dx élémentaires (considérés comme indivisibles donc)
=> il faut donc s’arranger pour que dans notre intégration avec dD, on retrouve l’élément vraiment élémentaire se cachant dans dD
=> la question n’est pas de savoir combien il y a de dR dans dD (cela serait une intégration donnant r²), mais comment varie D dans un R (c’est une sorte d’inverse (au sens courant)), dans la mesure ou l’on cherche le différentiel de base élémentaire avec lequel on va intégrer par la suite
=> c’est donc R=D/2, il faut dériver par D cette fois-ci, et on obtient 1/2, la facteur (multiplicatif) de correction pour [5] Vd2=pi/3*D^3 ? (dans la mesure que l’intégration d’un facteur consiste à une simple multiplication de l’intégration)
=> est-ce un raisonnement mathématiquement généralisable ?

Bonjour,
Quand vous intégrez la surface pour obtenir le volume, c'est par couches successives à partir du centre. La variable d'intégration part de 0 et va jusqu'à R, pas jusqu'à D....

J’aimerais revenir sur cela. Qu’est-ce qui vous permet spontanément de considérer que c’est à partir du centre ?

J’ai cela en tête : je réduis par commodité les dimensions, et de la sphère, je considère un cercle. Je fais la somme des segments horizontaux de longueur D variable discrétisant du haut en bas le cercle dans l’intention d’avoir la surface du dit cercle. D varie de 0 à D (partie 1 longueur des segments croissant) et de D à 0 (partie 2 longueur des segments décroissant). Pour calculer l’aire, il me faut intégrer la longueur des segments de la partie 1 (de 0 à D) (sans doute avec un cosinus je pense, il n’y a pas plus simple, non ?) et renoncer à la partie suivante, sinon en multipliant par 2 le résultat trouvé avec le traitement de la partie 1.
Dans cette vue d’esprit, il n’y a pas de considération pour le centre du cercle (ou sinon, si on cherche vraiment, comme quelque point d’un axe de symétrie miroir entre la partie 1 et la partie 2 ...)

[gg0]

Bonjour.

"D varie de 0 à D" ?? Le plus sûr moyen de se tromper en maths est d'utiliser la même lettre pour deux quantités différentes.

"Dans cette vue d’esprit, il n’y a pas de considération pour le centre du cercle (ou sinon, si on cherche vraiment, comme quelque point d’un axe de symétrie miroir entre la partie 1 et la partie 2 ...) " Ben si, c'est exactement ce que tu as fait. Et tu as même utilisé la symétrie à la fin : "en multipliant par 2 le résultat trouvé avec le traitement de la partie 1" (même si la formulation est bizarre avec "renoncer à la partie suivante" et surtout le surprenant "sinon". mais je pense avoir compris.

Cordialement.

[gg0]

Par ailleurs, pour "Qu’est-ce qui vous permet spontanément de considérer que c’est à partir du centre ? ", tu peux partir de l'extérieur, mais ce qui compte, c'est que les couches sont des espaces entre deux sphères concentriques, de centre le centre de la sphère, donc le centre joue un rôle "central" !

Par la suite, tu proposes une autre méthode, qui est de couper en tranches "planes". Pourquoi pas, mais alors tu as changé d'idée. Ce qui justifie que l'aire soit la dérivée du volume (pour une sphère) est justement la méthode des couches sphériques. Où la variable est le rayon des couches sphériques. Après, on peut vouloir changer le résultat en utilisant une autre variable, mais c'est finalement sans intérêt : Pas besoin d'intégration ou de dérivation pour exprimer volume et aire extérieure de la sphère en fonction du diamètre, seulement de R=D/2 et on remplace.

Finalement, depuis le début, tu cherches à généraliser un résultat très particulier, comme si c'était un exemple. Pourtant, dans le cas d'un cube, la dérivée du volume V(c)=c^3 en fonction de la longueur du côté est 3c², qui n'est pas l'aire latérale; ne parlons pas de volumes plus complexes ...

Cordialement.

[EspritTordu]

"D varie de 0 à D" ?? Le plus sûr moyen de se tromper en maths est d'utiliser la même lettre pour deux quantités différentes.

C’est en effet un bon conseil, merci bien !

Par ailleurs, pour "Qu’est-ce qui vous permet spontanément de considérer que c’est à partir du centre ? ", tu peux partir de l'extérieur, mais ce qui compte, c'est que les couches sont des espaces entre deux sphères concentriques, de centre le centre de la sphère, donc le centre joue un rôle "central" !

Si une boule est une somme de couches successives de sphères, il me faut n sphères de diamètre 0 à ValeurD pour la remplir, non... ?... À moins qu’il n’en faut que la moitié alors, c’est peut-être bien cela ?

Finalement, depuis le début, tu cherches à généraliser un résultat très particulier, comme si c'était un exemple. Pourtant, dans le cas d'un cube, la dérivée du volume V(c)=c^3 en fonction de la longueur du côté est 3c², qui n'est pas l'aire latérale; ne parlons pas de volumes plus complexes ...

Ce n’est que 3c²=Acube/2 après tout, à un facteur 2 près ... ? Mais je comprends ce que vous voulez-dire : si le volume du cube est perçu comme la somme de couches successives d’aire de carrés empilés l’un sur l’autre, alors il est difficile de comprendre qu’elle sens pourrait avoir la dérivée dans ce raisonnement. Il est tout de même intéressant de voir que le résultat n’est pas si loin numériquement. Il ne serait peut-être pas si inintéressant de voir quelle contorsion il serait nécessaire pour alors donner sens à la dérivée dans ce raisonnement pour retrouver le résultat attendu.

[MissJenny]

Pourtant, dans le cas d'un cube, la dérivée du volume V(c)=c^3 en fonction de la longueur du côté est 3c², qui n'est pas l'aire latérale; ne parlons pas de volumes plus complexes ...

mais si tu considères la distance entre le centre du cube et le centre d'une face, soit d, qui vaut donc c/2. L'aire d'une face est 4d^2 et donc l'aire du cube 6*4*d^2 = 24 d^2. Le volume, lui est (2d)^3 = 8 d^3. Si tu dérives par rapport à d tu retrouves bien l'aire.

[gg0]

Effectivement, MissJenny. Je le savais. Mais est-ce utile d'embrouiller encore EspritTordu ?

Cordialement.

[gg0]

EspritTordu :
"Si une boule est une somme de couches successives de sphères, il me faut n sphères de diamètre 0 à ValeurD pour la remplir, non... ?" ça veut dire quoi ce que tu racontes ? C'est qui, n? Et pourquoi parles-tu de "de 0 à D" ?
Je commence à penser que tu ne connais pas la preuve classique, que tu n'as jamais même fait ou vu le dessin de principe, que tu parles sans savoir. À quoi sert qu'on essaie de t'expliquer alors que tu parles dans le vide ?
Si tu prends des sphères de rayons allant de 0 à D, la sphère la plus extérieure a un rayon de D, et donc un diamètre de 2D, pas le bon !

[MissJenny]

Effectivement, MissJenny. Je le savais. Mais est-ce utile d'embrouiller encore EspritTordu ?

est-ce que ça l'embrouille? quand on utilise le côté c, c'est comme si les cubes emboîtés avaient tous un coin commun, et donc si l'accroissement ne se faisait que sur 3 faces, les 3 autres faces restant dans les trois plans qui s'intersectent au coin fixe. D'où le facteur 2.

[MissJenny]

pour illustrer ce que je disais plus haut, mais sur des carrés parce que c'est plus simple à dessiner. Le point important c'est qu'il faut faire la dilatation à partir du centre et pas d'un coin.

[gg0]

L'inconvénient de la sphère, c'est qu'elle n'a pas de coin (*). Mais cette propriété d'aire latérale dérivée du volume fonction d'un paramètre existe bien pour des volumes plus complexes que je ne chercherai pas à définir précisément, mais que je qualifierais bien de "en oignon" puisque leur volume est l'intégrale de couches superposées.
Sinon, j'ai effectivement l'impression que ET s'embrouille déjà lui-même en ne regardant pas les preuves des résultats qu'il utilise.

Cordialement.

(*) et pourtant, on dit "aux quatre coins de la planète"

[ThM55]

Je crois que le problème de compréhension vient d'une vision trop formelle de la relation entre le volume et l'aire au moyen de la dérivée. C'est plus clair effectivement avec la vision géométrique de la somme de couches sphériques, mais au départ EspritTordu voyait cela comme un simple problème de dérivées.

Pour rester dans ce registre formel, on peut résoudre ce problème en examinant la propriété de l'opération de dérivation pour les fonctions composées t alors la réponse devient évidente. Soit une fonction F définie sur et une fonction G définie comme la dérivée de F: . Je fais le changement de variable où k est une constante (par exemple un nombre entier, par exemple k=2). Comme fonction de y, on doit définir de nouvelles fonctions H et I définies par et de même .

Mais

Donc I n'est pas la dérivée de H. Au lieu de cela, on a . La question de réduit donc à une observation triviale sur l'opération de dérivée.

[EspritTordu]

C’est en effet un bon conseil, merci bien !
Si une boule est une somme de couches successives de sphères, il me faut n sphères de diamètre 0 à ValeurD pour la remplir, non... ?... À moins qu’il n’en faut que la moitié alors, c’est peut-être bien cela ?

Depuis le début on présente le cas comme si le cercle (je réduis les dimensions) que l’on dilate se trouve centré sur un centre O et que l’on l’étend suivant son rayon R depuis O. Cela me posait problème de considérer le diamètre et de finir par parler rayon.

Mon raisonnement est résumé par la première figure ou le diamètre D s’étend à gauche et à droite du centre O (il n’y a pas de rayon concerné) : on a des cercles imbriqués de diamètre chacun D1, D2, D3, D4, D5,...

Je simplifie le raisonnement d’intégration en considérant des couches successives comme des cercles d’épaisseur 1 fixe ; je cherche l’aire (ou le volume si on considère la dimension supérieure avec boule et sphère comme dans le cas initial de la discussion) du cercle n°5 de diamètre final Dfinal=10 (en noir sur la seconde figure de l’image que je décris) : combien de cercles d’épaisseur 1 et de diamètre Dn propre chacun, je peux placer dans le cercle noir ? Et bien la figure montre que seulement 5 peuvent être, soit la moitié de Dfinal effectivement. La valeur est identique au rayon, mais rigoureusement et conceptuellement, ce n’est pas le rayon. On ne dilate pas les cercles suivant le rayon selon ce raisonnement puisqu’il n’y a pas de rayon dans les hypothèses (on se l’interdit). On dilate suivant Dn, et pour chaque élémentaire Dn, on couvre systématiquement non pas 1 unité, mais 2 : une à gauche du centre O et une à sa droite.

Pour revenir au cas initial et au volume d’une boule calculé selon les couches successives de sphère de diamètre dD, je dois sommer (infiniment) dD de 0 à Dfinal/2 comme présenté précédemment effectivement. Mais ce n’est pas à proprement parlé le rayon, c’est simplement le nombre de sphères utiles dans une boule.
Or si j’intègre dD de 0 à D comme je le souhaitais au début, cela se traduit par le fait :
-soit (1) je calcule le volume d’une boule finale implicitement de diamètre 2D sans en avoir donc conscience,
-soit (2), si je me fixe bel et bien une boule de diamètre D (comme j’avais donc en tête), on peut le voir comme si je calcule 2 fois la même valeur : les parties de sphère à gauche (ou à droite) du centre, étant numériquement pris deux fois : on doit pouvoir considérer cela comme un cas de superposition : je me demande au fond si je fais bien de chercher à me représenter géométriquement cette superposition, et que je ne dois pas me contenter seulement de l’approche numérique...?
Pour l’interprétation de la dérivée deux fois plus petite qu’attendue (selon la lecture de (2)) cela ne correspond donc pas à l’aire d’une sphère d’une couche successive, comment alors l’interpréter alors en restant dans le cadre restrictif (2) ?

pour illustrer ce que je disais plus haut, mais sur des carrés parce que c'est plus simple à dessiner. Le point important c'est qu'il faut faire la dilatation à partir du centre et pas d'un coin.

Merci pour cette illustration. Bien que l’on parle de carré/cube plutôt que de cercle/sphère/boule, il me semble que le problème parait similaire en effet.
Seulement après le raisonnement (2) on l’on étend la forme géométrique prototype pour chercher son volume depuis le centre O avec son rayon, celui (1) dont je parle précédemment (celui que j’ai en tête pour la discussion) où l’on étend le diamètre de part et d’autre du dit centre O, vous me semblez en proposer un troisième ou l’on prend un point fixe et l’on étend non pas D de manière symétrique à O, mais c depuis le point fixe, un sommet du cube, non ? On grossit un cube depuis le point fixe, son sommet ?

Je ne comprends pas très bien le schéma de gauche : si on cherche le volume final d’un cube, l’intégration des cubes élémentaires croissants en volume jusqu’à la valeur finale conduit à ce que le sous-cube suivant recoupe le sous-cube précédent plus petit qu’il enveloppe ?

[EspritTordu]

Je crois que le problème de compréhension vient d'une vision trop formelle de la relation entre le volume et l'aire au moyen de la dérivée. C'est plus clair effectivement avec la vision géométrique de la somme de couches sphériques, mais au départ EspritTordu voyait cela comme un simple problème de dérivées.

Pour rester dans ce registre formel, on peut résoudre ce problème en examinant la propriété de l'opération de dérivation pour les fonctions composées t alors la réponse devient évidente. Soit une fonction F définie sur et une fonction G définie comme la dérivée de F: . Je fais le changement de variable où k est une constante (par exemple un nombre entier, par exemple k=2). Comme fonction de y, on doit définir de nouvelles fonctions H et I définies par et de même .

Mais

Donc I n'est pas la dérivée de H. Au lieu de cela, on a . La question de réduit donc à une observation triviale sur l'opération de dérivée.

Effectivement, en changeant de variable entre D et R, le facteur de valeur fixe entre R et D, se retrouve numériquement dans le jeu des dérivées comme un facteur multiplicatif, somme toute externalisé selon l’approche calculatoire.