Volume de l'intersection d'une sphère avec un tétraèdre

[invitee4ef379f]

Bonjour,

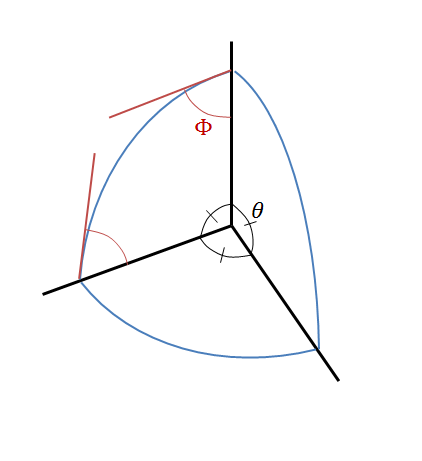
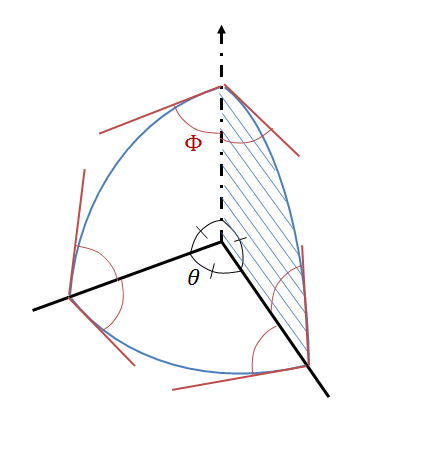
Dans le cadre de mes recherches sur la croissance de pores, je voudrais calculer le volume de l'intersection d'une sphère avec un tétraèdre (voir figure ci-dessous). Les angles du tétraèdre sont de 109,28 degrés. Le tétraèdre intersecte une sphère de rayon R mesurable. Les angles entre les tangentes à la sphère aux points d'intersection, dans les plans des côtés du tétraèdre, et les arètes du tétraèdre, sont mesurables et partout égaux.



Je parviens à calculer les surfaces d'intersection dans les plans des côtés du tétraèdre, mais le volume est récalcitrant!

Une idée?

Merci d'avance.
-----

[Médiat]

Bonjour,

Je parviens à calculer les surfaces d'intersection dans les plans des côtés du tétraèdre, mais le volume est récalcitrant!

Si vous savez calculer la surface en fonction des angles, par exemple , il n'y a plus qu'à intégrer entre 0 et (par calcul de primitive ou calcul numérique)

[invitee4ef379f]

Entre 0 et?

Je sais calculer l'aire de la surface hachurée sur le schéma suivant:



Comme mentionné, tous les angles sont égaux. Il n'y a donc pas nécessairement de symétrie par rotation autour d'une des arêtes du tétraèdre (ligne discontinue sur le schéma par exemple). Je ne peux pas intégrer sur .

Je ne parviens pas à voir comment une intégration sur peut me donner le volume requis. Pouvez-vous développer un peu plus?

Merci d'avance.

[invite7c2548ec]

Bonjour:

Le mieux c'est de compléter la figure par la nomination des sommets de cette tétraèdre , car le calcule de volume sur utilise les intégrale triples et ce calcule dépend immédiatement du domaine de définition du volume en sujet , plus l’aspect géométrique de cette figure est claire plus en économise du temps à arriver aux résultat .

Cordialement

[A voir en vidéo sur Futura]

[invitede656be3]

Bonsoir,
Ta figure semble avoir un axe de symétrie d'ordre 3 (rotation de 120°) selon un axe qui joint le centre de la sphère et l'intersection des 3 arêtes (angles et arêtes égaux).
Je ne vois pas comment la 4^ème face du tétraèdre (un plan) peux couper une sphère autrement que par un cercle.
Ou alors c'est un tétraèdre auquel on rajoute un "bout" de sphère, comment se raccordent-ils.
Comme l'a dit "topmath" tu ferais bien de faire une figure correcte même si l'art de la géométrie est de raisonner juste sur une figure fausse.
On ne peux pas t'aider si tu ne donne pas suffisamment de renseignements sur la géométrie de ton modèle.
Cordialement.