Bonjour,
Dans cet algorithme j’ai utilisé une formule pour rechercher les nombres premiers.
A vous de juger s’il vous plaît, merci
Ci joint une copie d’ecran:Code:#include <stdio.h> #include <stdlib.h> #include <new> int main() { int N=0,compteur=1, x=1; int val ; printf ( "Programme Personnel basé sur le programme de recherche des NP à partir des carrés des precurseurs aux NP. \nVeuillez insérer un nombre limite en dessous duquel tous les nbres premiers seront calculés : " ) ; scanf("%d", &val); bool * Tableau2 = new bool [val]; while ( compteur >0) { for (int y =0 ; N < val ; y++) { N = 4*x*x + 4*x + 1 + y*(4*x + 2); // formule utilisée Tableau2[N]=1; compteur = y ; } x++; N = 0; compteur--; } for (int i =3; i < val; i = i+2) { if (Tableau2[i]==0 ) { printf(" %d", i); } } }
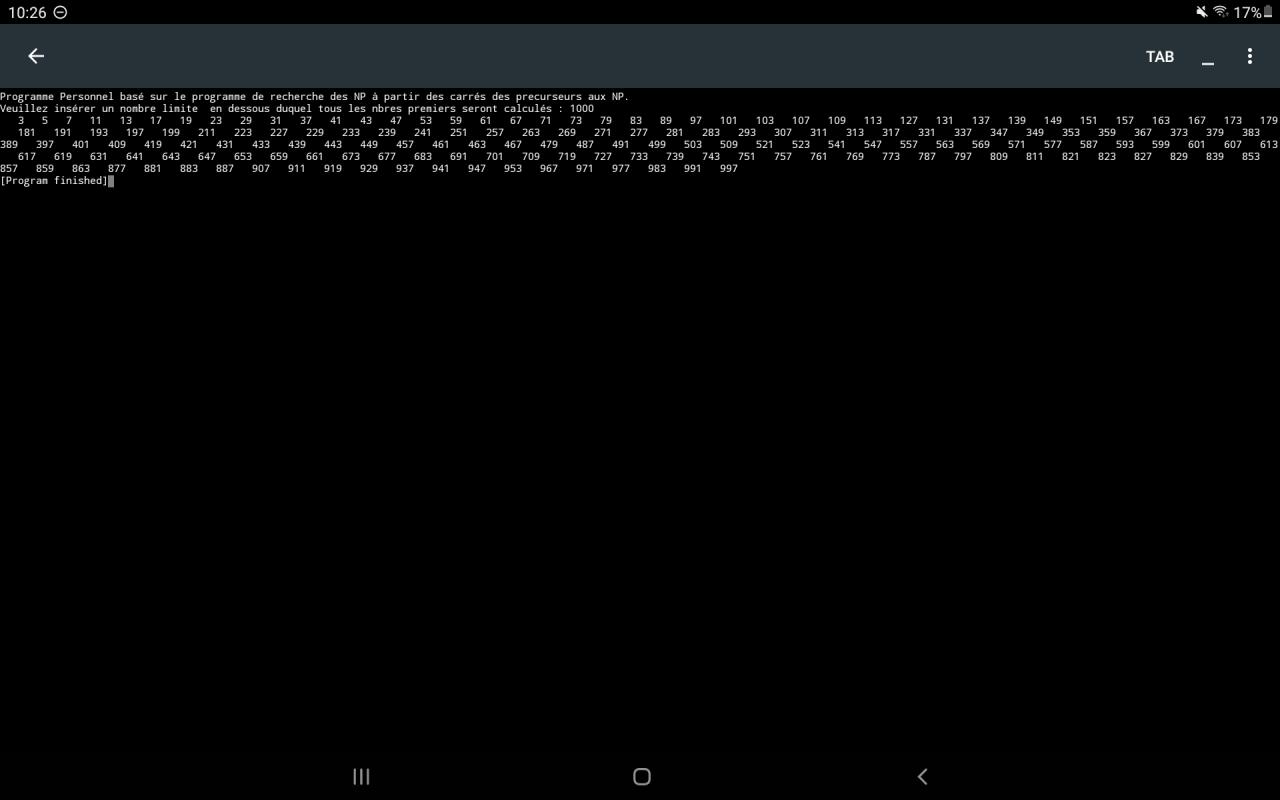
-----




 , et on a rarement besoin de listes de petits nombres premiers.
, et on a rarement besoin de listes de petits nombres premiers.

 ! C'est chronophage ce genre de truc, et vous aussi si on pense, au final, vous recevez une réponse désagréable d'un gars, qui n'est pas un Ramanujan (ça c'est une évidence
! C'est chronophage ce genre de truc, et vous aussi si on pense, au final, vous recevez une réponse désagréable d'un gars, qui n'est pas un Ramanujan (ça c'est une évidence