bonjour à toutes et à tous dans le cadre de mon stage je dois résoudre une équation intégral pour déterminer une force appliquer à un rouleau cylindrique et
sa fait un moment que je suis bloqué alors aider moi à y voir un peu plus claire SVP
voilà le problème
Po=une fonction (en faite c'est une pression)
[1-(x²/a²)]^(1/2) est une seconde fonction
j'ai pensé à l' IPP mais je je trouve pas le bon resultat donc je sais plus comment résoufre cette équation.
-----




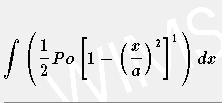
 est une constante quelconque (ainsi que
est une constante quelconque (ainsi que 
