Bonjour, je suis un pauvre lycéen en 1° STG avec toute l'incompetence que cela entraîne. (donc ne déballez pas toute votre science d'un coup sinon je serai perdu^^)
En fait j'aimerai savoir comment trouver une fonction avec des coordonnées. J'ai survolé le forum et j'ai vu que vous parliez des polynomes de lagrange dans un sujet, mais cette méthode ne me convient pas parce qu'en dehors des points aparement le tracé part dans tous les sens.
En lisant un peu plus loin j'ai aperçu une phrase parlant d'exponentielle qui ne passerai pas forcement pile poil par tous les points mais qui serait plus apte à définir la tendance futur de la courbe.
Donc ma question est : commment ksa marche le/a "truc" exponentielle ?
Merci

-----





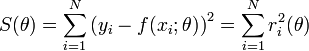
 ): madjes dit que sa fonction correspondant à un indice boursier. Mais les variations d'un indice boursiers ne sont-elles pas largement "aléatoires"? Peut-on réellement espérer les prévoir?
): madjes dit que sa fonction correspondant à un indice boursier. Mais les variations d'un indice boursiers ne sont-elles pas largement "aléatoires"? Peut-on réellement espérer les prévoir? 


