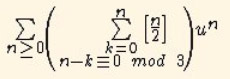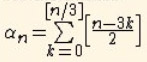series entieres

[invite94e19ae9]

Bonjour,
Je revise un peu les series entieres pour les concours (j'en ai bien besoin apparement ) et je suis tombé sur un exo que je comprends que dalle ...
Pouvez vous m'aider ?

(1) Developper en serie entiere la fraction rationnelle :
En déduire la valeur de où est le nombre de points entiers naturels (x,y,z) vérifiant : 2x+4y+6z=n.

(2) Quel est le rayon de convergence de cette serie . Quelle est la nature de la série

(3) Comment calculer, b_n , le nimbre de points entiers naturels (x,y,t,z) vérifiant : 2x + 7y + z + 3t = n

Merci de votre aide...
-----

[martini_bird]

Salut,

je propose une solution, pas très "astucieuse", mais qui fonctionne: en posant u=t², la série cherchée est le triple produit



Or


et

d'où les coefficients:


Celà répond à la première partie du 1).

Je te laisse chercher la suite (il faut utiliser le triple produit ci-dessus).

A+

[invite94e19ae9]

Merci pour ta réponse , je v essayer de comprendre tout ca et de faire la suite ...
Merci
a+++

[Gwyddon]

en scindant la fraction en 1/(1-t^2), 1/(1-t^4) et 1/(1-t^6) avec quelques coefficients derrières, on peut s'en sortir non ?

[A voir en vidéo sur Futura]

[martini_bird]

en scindant la fraction en 1/(1-t^2), 1/(1-t^4) et 1/(1-t^6) avec quelques coefficients derrières, on peut s'en sortir non ?

Salut,

hum, m'est avis qu'il faudrait que tu revoies la décomposition d'une fraction rationnelle en éléments simples.

Cordialement.

[Gwyddon]

Salut,

hum, m'est avis qu'il faudrait que tu revoies la décomposition d'une fraction rationnelle en éléments simples.

Cordialement.

grr...

m'est avis que tu n'as pas compris ma démarche. Je ne voulais pas décomposer en élément simples, du moins pas jusqu'au bout, je voulais juste scinder en petits morceaux pour avoir des termes développables aisément.

Bon je fais le calcul et je reviens te montrer ce que je souhaitais faire

[Gwyddon]

hum, m'est avis qu'il faudrait que tu revoies la décomposition d'une fraction rationnelle en éléments simples.

ok j'ai compris pourquoi tu dis ça, quand je parlais des coefficients, ces coefficients dépendaient aussi de x, x^2, etc...

[martini_bird]

grr...

m'est avis que tu n'as pas compris ma démarche.

Ben, tu voulais décomposer la fraction sous la forme
?

Je ne voulais pas décomposer en élément simples, du moins pas jusqu'au bout, je voulais juste scinder en petits morceaux pour avoir des termes développables aisément.

Bon je fais le calcul et je reviens te montrer ce que je souhaitais faire

J'attends...

Amicalement.

[Gwyddon]

bon c'est infernal, tout aussi compliqué sinon plus que ta méthode, on oublie ma proposition (mais note bien qu'elle fonctionne, elle amène juste à résoudre un système de 9 équations à 9 inconnues...)

[martini_bird]

J'ai compté douze inconnues car

et donc


Bref, c'est clair que c'est faisable, mais après tu fais quoi des derniers termes ?

[Gwyddon]

salut,

bon en fait ma démarche ne fonctionne absolument pas... Je vais montrer ce que je souhaitais faire avec c'est moins long à écrire ;

L'idée était d'écrire et de calculer les bon coefficients.

Je ne voulais donc pas décomposer en éléments simples (car je sais qu'il reste des termes que je sais pas développer). Mais ça ne va pas, donc mea culpa pour avoir bêtement insisté.

[Gwyddon]

bon je ne vois rien d'autre que les produits de cauchy de martini_bird, si quelqu'un a une autre solution plus élégante, qu'il n'hésite pas

[invite94e19ae9]

salut !
je comprends pas le cheminement pour arriver au produit triple que martini_bird a proposé...

[Gwyddon]

tu sais (car tu connais tes DSE classiques...) que pour |t| < 1 on a


Tu constate ici que pour |t|<1 tu as aussi , donc tu as :



la suite, c'est martini_bird

@+
julien

[invite94e19ae9]

A ouiiiiiiiiii je suis trop bete ! merci bien ....

[invitea2d3d62b]

Je fais un peu remonté un vieux sujet, mais je revise avec r-one, donc on a bloqué tt les deux sur l'exo, j'ai posté aussi ce sujet sur un autre forum, et il semble que les reponses different legerement.

on me propose pour la serie entiere

avec E(k/2) + 1 dans la somme.

et pour :

la meme chose plus E(n/3) + 1

[martini_bird]

Salut,

j'ai vérifié mes calculs, ma formule est correcte (sauf si je me suis trompé ).

Il faut être soigneux, mais il n'y a pas de difficulté conceptuelle: il suffit d'appliquer la règle pour le produit de deux séries.

Cordialement.

[matthias]

On est d'accord.

Il me semble que :

J'ai donc:

Ce qui donnerait:


Il est tout à fait possible que je me trompe. Si c'est le cas pouvez-vous me dire où et pourquoi ?

[martini_bird]

Tu as raison, matthias.

Salut,

j'ai vérifié mes calculs, ma formule est correcte (sauf si je me suis trompé ).

Je me suis trompé.

Il faut être soigneux, mais il n'y a pas de difficulté conceptuelle: il suffit d'appliquer la règle pour le produit de deux séries.

Pour le soin, je repasserai!

A+

PS: Il n'y a pas de smiley avec un bonnet d'âne...

[matthias]

Tu as raison, matthias.

Je n'étais pas vraiment sûr...

PS: Il n'y a pas de smiley avec un bonnet d'âne...

Aucune raison, c'est en essayant de comprendre tes calculs quand la question est apparue sur un autre forum que j'ai été étonné de trouver un résultat légèrement différent.

Sinon je me suis amusé à calculer les coefficients , je ne suis pas sûr que ce soit utile, ça donne un truc assez ignoble, mais je vais le poster pour avoir un avis.

[matthias]

On a donc:


En utilisant:


Je trouve ce truc ignoble:


Et comme je n'avais vraiment rien à faire, j'ai poussé un peu plus loin: