Bonjour à tous,
Je suis actuellement en stage et je fait de la modelisation moléculaire en étudiant des pharmacophores. Et j'aurai une petite question à vous poser car mon niveau de 3D est relativement limité.
Mon probleme est le suivant : J'ai une ellipsoïde dont je connait les 3 axes x, y et z qui la définisse et ainsi que la longeur des demi axe a,b,c. Tout les points apartenant à la surface de l'ellipsoïde verifie donc l'equation x2/a2+y2/b2+z2/c2=1
Je cherche à inclure cette ellipsoïde dans un cylindre sachant que l'axe d'orientation du cylindre et donné sous forme d'un vecteur dont les coordonnées sont données par un utilisateur. Cette axe peut donc etre orienté de toutes les manières possibles dans l'espace.
Mais alors comment obtenir le rayon R du cylindre? sachant que je connait le vecteur d'orientation de l'axe du cylindre et les coordonnées qui definisse mon ellipsoïde.
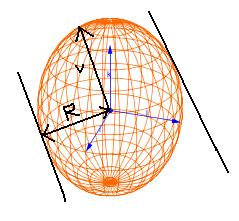
regardé l'image ici qui je pense defini bien mon probleme :
Voila la solution à laquelle j'ai pensé :
J'appelle H le centre de mon ellipsoïde de coordonnées Xh,Yh,Zh que je connais
L'axe de mon cylindre et definie par le vecteur v centrée sur H de coordonnée : (Xh-Xv);(Yh-Yv);(Zh-Zv) c'est coordonnées sont également connue
Je cherche donc ici la distance R entre le point H et l'instersection de la droite R avec la surface de mon ellipsoïde notons ce point E de coordonées Xe,Ye,Ze. Je cherche donc les coordonnées du point E pour calculer la distance HE.
Il me faut alors un systeme à trois equations :
(1) E apartient à la surface de l'ellipsoîde et donc verifie l'equation :
Xe2/a2+Ye2/b2+Ze2/c2=1
(2) les vecteurs V et R sont orthogonals et donc verifie :
(Xh-Xv)(Xe-Xh)+(Yh-Yv)(Ye-Yh)+(Zh-Zv)(Ze-Zh)=0
(3) le vecteur V à une longueur connut et donc si je change l'origine de V centrée en H sur le point E on a :
racine((Xe-Xv)2+(Ye-Yv)2+(Ze-Zv)2)=racine((Xh-Xv)2+(Yh-Yv)2+(Zh-Zv)2)
J'ai donc un systeme d'equation à trois inconnue avec Xe,Ye et Ze à resoudre pour trouver les coordonnée du point E et ensuite calculer la distance R egale à EH.
Je n'ai aucune idée si ce que j'ai fait est correcte et surtout comment resoudre ce systeme un peu complexe si des âmes charitable voudrait me filer un coup de main ce ne serait pas de refus.
Je vous remercie d'avance pour vos réponses.
Madsnake
-----