Bonjour à tous,
J'ai un devoir à effectuer dont voici une partie de l'énoncé :
J'ai trouvé facilement la réponse à la première question (l'aire vaut PI/4), mais la deuxième question me pose problème. En effet, j'ai utilisé la relation qui donne :Utiliser la fonction f(x)= sqrt(1-x²) sur l’intervalle[0;1].
Géométriquement, sans calcul d’intégrales, que vaut l’aire sous la courbe de f sur [0;1] ?
Construire une somme de Riemann à l’aide de cette fonction et donner alors une formule de calcul qui approche la valeur de PI/4.
où
Comme ici les bornes de l'intégrale sont a=0 et b=1, cela simplifie légèrement la formule, mais je ne vois pas quoi faire sur cette formule pour obtenir une approximation de PI/4.
J'aurais donc besoin d'aide sur cette question. Une piste ou quelques indications seront donc les bienvenues.
Merci d'avance !
-----




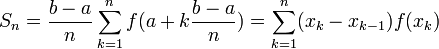
 ? Par quoi peut-tu l'encadrer (cf Darboux) ? Tu pourrais passer en coordonnées polaires, ça se voit encore mieux.
? Par quoi peut-tu l'encadrer (cf Darboux) ? Tu pourrais passer en coordonnées polaires, ça se voit encore mieux.

