Propriétés de la fonction phi d'Euler
Discussions similaires
-
Par invitee51caab2 dans le forum Mathématiques du supérieur
Réponses: 4
Dernier message: 14/05/2008, 23h29
-
Par invite5e5dd00d dans le forum Mathématiques du supérieur
Réponses: 6
Dernier message: 07/03/2008, 10h44
-
Par invite43bf475e dans le forum Mathématiques du supérieur
Réponses: 2
Dernier message: 17/11/2007, 13h43
-
Par invite8c3060a6 dans le forum Mathématiques du supérieur
Réponses: 0
Dernier message: 22/02/2007, 11h38
-
Par invite0f71df23 dans le forum Mathématiques du supérieur
Réponses: 9
Dernier message: 29/01/2007, 08h58
suivante sachant que
est premier :
(avec k une constante entière)







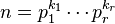 )
)