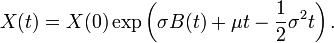Résolution d'équation différentielle stochastique

[inviteab667d05]

Bonjour,

Je cherche à résoudre numériquement une équation différentielle stochastique de la forme



où représente un mouvement brownien ( suit une loi ).

Comme je n'y connais rien, j'ai cherché et vu qu'il existe différentes méthodes adaptées aux EDS : Euler-Marayuma, Milstein, Runge-Kutta ... Mais j'ai quelques questions.

Ce que j'essaie de faire, c'est d'appliquer une méthode classique en écrivant l'EDS comme une EDO :

(*)

où est un bruit blanc gaussien ( suit une loi )

(Je n'ai pas trop le droit car n'est pas smooth, mais bon)

En discrétisant (*) avec Euler explicite classique, on obtient :



et en écrivant ( est supposé assez petit), on tombe sur la formule d'Euler-Maruyama :



---
J'ai testé le schéma sur l'équation :

, ,

pour laquelle on connaît la solution analytique :



et j'obtiens comme attendu le même résultat ( étant fixé) pour Euler-Marayuma appliqué directement à l'EDS et Euler explicite appliqué à la forme "EDO" :

, ,

les deux résultats sont très proches du résultat analytique. ( assez petit).

--
J'ai donc voulu faire la même chose avec Runge-Kutta ordre 2 appliquée à la forme "ODE" i.e. :

pour , on applique les étapes :




[/TEX]

Mais en utilisant ceci, je n'obtiens pas un résultat proche de la solution analytique.

En cherchant sur internet, j'ai trouvé qu'on pouvait définir deux types de solutions (Itô ou Stratonovich) et que les schémas Runge-Kutta conduisaient à la solution Stratonovich donnée en utilisant les règles de calcul classique








mais même avec un pas de temps très petit, la solution que j'obtiens avec RK2 ne se rapproche pas de cette dernière solution.

--
Mes questions :

- Est-ce que ça a un sens d'appliquer une méthode classique à la forme "EDO" d'une "EDS" ?
- Le fait que Euler-explicite donne Euler-Maruyama est-ce une coincidence ? (surtout qu'apparemment l'ordre de convergence forte d'Euler-Maruyama est 1/2 et pas 1, Milstein corrige ça en introduisant un terme correctif ...)

Merci d'avance de votre aide. J'ai trouvé beaucoup d'informations sur internet, mais c'est un peu le bazar dans ma tête.

Merci encore.
-----

[inviteae4072e1]

En général, dans ce genre d'exercice (en Finance par exemple) on utilise la formule d'Ito (sous condition des fonctions f et g) afin d'obtenir un résultat. Comment peux-tu dans ton exemple dire que dWt/dt est un BB gaussien centré de variance 1/dt ?

[inviteab667d05]

Merci de la réponse,

Pour , j'utilise le fait que suit , donc suit . A-t-on le droit d'écrire ça ?

En finance, travaille-t-on directement sur l'équation ? et quels schémas numériques utilise-t-on ?

Merci encore.

[inviteae4072e1]

En fait résoudre l'équation :



Ou B est ton Mouvement Brownien, passe par la formule d'Itô appliquée à la fonction ln (de classe C2, toussa toussa) ce qui donne :



c'est-à-dire après intégration :

[A voir en vidéo sur Futura]

[inviteae4072e1]

Concernant la loi normale (Brownien) de variance 1/dt, cela est faux je pense...

[inviteab667d05]

En fait résoudre l'équation :



Ou B est ton Mouvement Brownien, passe par la formule d'Itô appliquée à la fonction ln (de classe C2, toussa toussa) ce qui donne :



c'est-à-dire après intégration :

Oui oui, j'avais vu que c'était comme ça qu'on déterminait la solution au sens d'Itô.

Concernant la loi normale (Brownien) de variance 1/dt, cela est faux je pense...

Ok, ça veut dire que je n'ai pas le droit d'utiliser Runge-Kutta classique sur la forme "ODE" où intervient ? et que Euler explicite était juste une coïncidence ?

même si en version discrète, en écrivant Euler-Maruyama



en définissant ,
c'est comme si on simulait un bruit blanc ("dérivée" d'un mouvement brownien) comme étant de variance non ?

En fait, je résous un problème où suit (perturbation pour prendre en compte la diffusion) en utilisant Runge-Kutta, et je voudrais savoir si ça avait un sens, ou dois-je passer à des méthodes "EDS" ?

[inviteab667d05]

En fait lorsque j'utilise Runge-Kutta 2, ça revient à :








et j'aurai tendance à dire que ça n'a pas trop de sens, je ne vois pas en quoi ce serait une approximation de :



Donc j'aimerais bien avoir une réponse catégorique qui me dise que je peux continuer à utiliser Runge-Kutta 2 sur la forme EDO (même si la variance "" est un peu bizarre ... surtout fausse) ou que je dois arrêter ce massacre et utiliser un schéma EDS sûr.

Merci d'avance.