Modèle mathématique décrivant l'évolution au cours du temps d'une grandeur physique

[manos59]

Bonjour,

J'ai besoin d'aide pour trouver une fonction f(t) capable de d'écrire l'évolution temporelle d'une grandeur physique.
Je dispose pour cela une courbe (obtenue à partir des simulations numériques), la courbe se trouve en fichier joint.
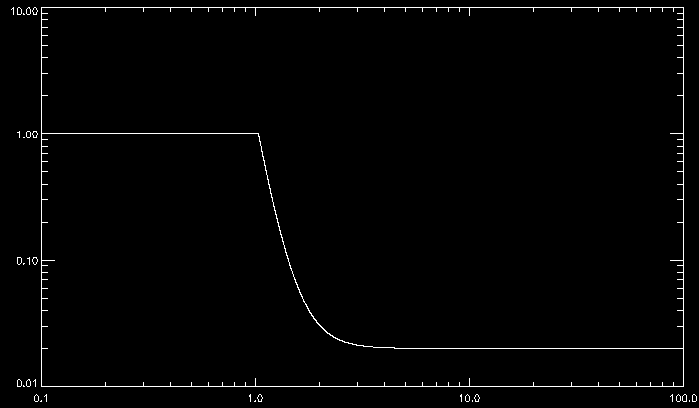
Globalement, je distingue trois zones sur cette courbe :
- une première zone constante allant de (t=t0 à t=t1) (où la valeur initiale f0) reste constante jusqu'à t=t1. Une fonction f(t)=f0 conviendrait
- une deuxième zone (de t=t1 à t=t2) ou l'évolution ressemble à une décroissance exponentielle, cette zone peut être d'écrite par une fonction du type f(t)=f0*exp(-at)
- une troisième zone (de t=t2 à t=tf) ou l'évolution est "stationnaire", la grandeur physique étudiée tend vers une valeur asymptotique fs (qui est une valeur d'intérêt pour moi), la fonction ressemblerait donc à quelque chose du type f(t)=fs.

L'intérêt de disposer de cette fonction f(t) décrivant l'évolution temporelle de ma grandeur physique est de pouvoir faire une prédiction connaissant f0.

Connaissant l'allure de la fonction, je pourrais procéder à des ajustements pour déterminer et caler les éventuelles constantes.

Quelqu'un peut-il m'aider à définir cette fonction?

D'avance merci pour votre aide.
-----

[invitefb0f1e11]

Salut,

j'arrive pas à accéder à la pièce jointe.

Mais tu n'as aucun indice "physique", sur la forme de la fonction ?

Si tu as un truc de la forme : constant - décroissant - constant.
Tu peut essayer de l'ajuster avec une truc de la forme :


Mais après rien ne dit que cela constituera une bonne approximation.
Si ton but est de faire une prédiction de la valeur de ta variable le mieux est peut-être de conservé la courbe et d'en faire une interpolation au valeur voulu .

Sinon tu peut toujours essayer d'ajuster ta courbe avec une série de lois de puissance.

Bonne chance,
@+,
G.

[manos59]

Bonjour et merci pour ta réponse,

La pièce jointe est(devient) en principe accessible, je viens de tester, peut-être qu'une validation de la pièce jointe par les modérateurs était nécessaire...
"L'indice physique" ou plutôt la réponse physique je l'ai, c'est avec les couple (t,f(t)) que j'ai obtenu la courbe dont je recherche la fonction. f(t) étant obtenue par simulations numériques.

Le problème consiste à étudier l'évolution de f (la température par exemple--> le refroidissement dans ce cas si l'analogie peut se faire) en fonction du temps.

Je précise que je ne connais que f0 à t=0.

Ta fonction peut décrire les deux dernières parties ma courbe (décroissant-constant) mais pas la première partie (constante).
La courbe ressemble à la figure ci-dessous si ça peut aider dans le raisonnement. Je souhaite prédire la valeur de fs.

    ^ f(t)/f0
     !
     !
  f0!****************************
     !                              *
     !                                *
     !                                  *
     !                                    *
     !                                      *
     !                                        *
     !                                          *
     !                                            *
fs   !                                              ******************************** fs
     !
     !
     !
     !-------------------------------------------------------------------------------->t
     t=0                       t1                 t2

Merci bien.

[invitefb0f1e11]

Re,

Je te conseille d'utilisé une truc de la forme :



où est une fonction composé de plusieurs loi de puissance ajusté pour fitter la courbe. Vu la tête de la courbe (c'est bon je peut voir a pièce jointe), je dirais que 3 loi de puissance devrait suffire
Donc pour g(x) essaie un truc de la forme


C'est pas garantie que le résultats soit super, mais c'est une fonction comme une autre .

Après vu la cassure dans l'allure de la courbe, ça va être dur d'obtenir le même effet avec une fonction "simple"

@+,
G.

[A voir en vidéo sur Futura]

[Bruno]

Bonjour,

Vu la tête de la courbe, ça ressemble à la réponse d'un système du premier ordre avec délais, à une entrée en échelon. C'est quoi votre système ? Il a une entrée connue ?

[manos59]

Bonjour,

Merci pour vos réponses, les fonctions proposées précédemment ne conviennent pas.


Le problème consiste à étudier l'agglomération/la dés-agglomération d'une suspension de fines particules (dans le cas étudier ici, il s'agit de la désagglomération--> fragmentation d'un agglomérat au cours du temps).
Au départ, mon système est constitué d'un seul agglomérat contenant N particules élémentaires sphériques (de taille micronique et mono-taille), l'agglomérat est immergé dans un fluide newtonien (de l'eau), puis cisaillé à un gradient de vitesse donné. La suspension est diluée (fraction volumique solide très très faible).

Le bilan des forces me conduit à ne retenir que les forces significatives suivantes:
-forces de van der Waals (forces attractives)
-forces hydrodynamiques (forces de Stokes)--> forces destructrices (responsable de la fragmentation)
-forces volumiques (gravité, poussée d'Archimède)--> négligeables d'ailleurs par rapport aux autres forces, vu la taille des particules
-les forces de contact (normales élastiques, normales dissipatives, tangentielles, friction, roulement)

J'applique une méthode appelée "Méthode des éléments discrets" qui est une "adaptation" de la méthode de "Dynamique moléculaire" aux corps macroscopiques.
J'étudie le mouvement des particules à partir de la seconde loi de Newton (application du principe fondamental de la dynamique). Les équations à résoudre numériquement, sont des équations différentielles du second ordre :

Pour le mouvement en translation :


où est la masse d'une particule primaire, est le vecteur vitesse en translation de la même particule et est la résultante de toutes les forces normales et tangentielles agissant sur la particule .



où est le moment d'inertie au centre de la particule , est le vecteur vitesse rotation et est la résultante de tous les moments agissant sur la particule .

Cette équation est ensuite résolue via un schéma d'intégration explicite de type Euler d'ordre 2.

Sous l'action des forces hydrodynamiques (fluide) et lorsqu'elles sont dominantes par rapport aux forces de cohésion (van der Waals), l'agglomérat initial formé de N particules élémentaires se fragmente en n flocs composés de ni particules élémentaires. J'ai par ailleurs montré et en accord avec les observations expérimentales qu'un équilibre s'établi entre les forces destructrices (hydrodynamiques) et les forces qui assurent la cohésion entre particules à l'intérieur d'un floc (van der Waals). Cet équilibre entre l'agglomération et la fragmentation conduit à une taille limite (nombrede particules élémentaires par floc) des flocs (on arrive plus à casser).

La courbe ci-dessous représente le nombre moyen de particules élémentaires par floc (normalisé par rapport au nombre de particules élémentaires de l'agglomérat initial) en fonction du temps (normalisé par rapport au temps caractéristique de cisaillement).

La moyenne , est une moyenne arithmétique classique définie par l'équation suivante :



où est le nombre total de flocs dans le système (la suspension), le nombre de particules élémentaires par floc.

J'espère que vous y voyez un peu plus claire sur le type de problème et sur ma motivation.

Merci à tous.

[invitefb0f1e11]

Étrange ...

Avec mon truc de la forme :


pour



J'obtiens un truc déjà vachement ressemblant ... alors en ajustant les paramètre, ça devrait sans être parfait au moins être une approximation raisonnable


@+,
G.

[manos59]

Merci.
Effectivement ta fonction peut décrire raisonnablement la courbe simulée ci-dessus (courbe tronquée).
J'ai utilisé gnuplot pour fiter mais il trouve une matrice singulière et je ne peux utiliser toutes les données car limitation.
Je vais essayer de trouver un autre outil si je n'y arrive pas avec gnuplot.

Quelle méthode as-tu utilisée pour trouver cette fonction?

Merci à toi.

[manos59]

Finalement, j'ai réussi à ajuster le modèle avec les résultats des simulations numériques à l'aide de gnuplot par tâtonnement au niveau de l'initialisation des paramètres. Merci pour ton aide et si tu peux m'expliquer le raisonnement qui t'as conduit à la définition de cette fonction ça me sera d'une grande utilité car j'ai d'autres comportements physiques dont je souhaiterai décrire par un modèle mathématique plus ou moins simple.

Merci.