Série de fourier

[narakphysics]

Bonjour à tous et à toutes
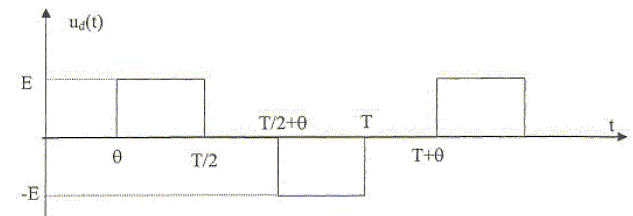
j'aimerai bien vérifier mes résultats concernant la série de fourier du signal suivant:

Voilà ce que j'ai trouvé:
d'après la figure on constate que le signal est impaire donc:

avec : et
or:
d'où:
Est ce juste?
merci d'avance
-----

[phys4]

avec : et
or:
d'où:
Est ce juste?

Bonjour,
Il manque des termes :
1- l'intégration doit se faire sur une période complète pour avoir tous les termes, en prolongeant à 2\pi vous allez voir que des termes disparaissent suivant leur parité.

2- évitez d'utiliser des constantes dans les variables de vos intégrales, cela vous évitera des pièges, ici il faudrait écrire

[narakphysics]

Merci de votre réponse

Bonjour,
Il manque des termes :
1- l'intégration doit se faire sur une période complète pour avoir tous les termes, en prolongeant à 2\pi vous allez voir que des termes disparaissent suivant leur parité.

Oui j'ai oublié la période !! je doit rajouter , l'expression de devient:
En ce qui concerne la parité, le signal est impair, donc le terme est nul

2- évitez d'utiliser des constantes dans lesvariables de vos intégrales, cela vous évitera des pièges, ici il faudrait écrire

Les deux intégrales ont la même surface ,donc :

[phys4]

Les deux intégrales ont la même surface ,donc :

Ce serait vrai, si sin(nt) prenait des valeurs opposées dans les intégrales, or le signe relatif des intégrales ne dépendrait-il pas de
la parité de n ?

[A voir en vidéo sur Futura]