Optimisation

[invite44e97bac]

Bonjour!

Désolé de vous déranger... Avant tout!
Ensuite, j'aimerai que vous m'aidez pour un exercice.
Pas que vous me donnez des réponses mais des pistes.
J'ai avancé mais je bloque tout de même sur certains points.

Ennoncé:

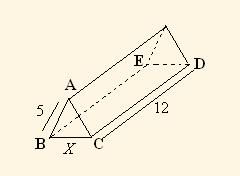
Un couloir entre deux bâtiments a la forme d'un prisme droit dont 2 des faces sont deux immenses baies
vitrées rectangulaires de 20 mètres de long sur 5 mètres de large.



Une section de ce prisme par un plan perpendiculaire à la face BCDE est le triangle ABC:
la longueur BC = x représente l'écartement des deux baies vitrées et le but de ce problème
est de déterminer x tel que le volume de ce couloir soit le plus grand possible.

1. a) Quelles sont les valeurs possibles de x?
J'ai fait l'inégalité triangulaire et je trouve [0;10]

1. b) Exprimez l'aire du triangle ABC en fonction de x.
J'ai utilisé le théorème de Pythagore dans le triangle ABC pour trouver la hauteur AF (J'ai nommé le point)
Puis j'ai trouvé racine carré de (5 + x/2) (5 - x/2)

Puis pour l'aire j'ai utilisé la formule B x H / 2
ce qui revient à X x racine carré de (5 + x/2) (5 - x/2) / 2
Je développe le tout? Et je réduis?

1. c) Exprimez le Volume V du prisme en fonction de X.
Je connais la formule c'est BC x AF / 2 x BE
Le problème c'est que je dois utilisé le résultat précédent.

2. Soit la fonction définie sur [0;10] par: f(x)= x² (100-x²)

a) Etudier les variation de f.
J'ai fais la dérivée de cette fonction et je trouve
f'(x)= 200X - 4x³

Merci d'avance...
Je répète pas de réponses que des pistes les autres questions j'essaierai de me débrouiller...
-----

[invite44e97bac]

Désolé j'ai pas trouvé "Editer". désolé pour ce double post.

1. b) Exprimez l'aire du triangle ABC en fonction de x.
J'ai utilisé le théorème de Pythagore dans le triangle ABC pour trouver la hauteur AF (J'ai nommé le point)
Puis j'ai trouvé racine carré de 100 - x²/2
J'ai réduis.

Puis pour l'aire j'ai utilisé la formule B x H / 2
ce qui revient à X fois racine carré de 100 - x²/2
Voilà j'ai débloqué ici.

1. c) Exprimez le Volume V du prisme en fonction de X.
Je connais la formule c'est BC x AF / 2 x BE
Donc ce qui revient à X fois racine carré de 100 - x²/2 fois 20

Corrigez moi si je me trompe... merci d'avance.

[invitecaff288f]

Salut,
le volume correspond a l'aire de la base*hauteur.
l'aire du triangle ABC en fonction de x
Aire(base)= racine carré de (100 - x^2)/2
donc volume=Aire(base)*H.
corrige ta question 1c

pour le reste, ca semble bon.

Bon courage

[invite44e97bac]

C'est plutôt bizarre (désolé) mais racine de 100-x²/2 c'est plutôt la hauteur et non la base, non?

[A voir en vidéo sur Futura]

[invite44e97bac]

1 c) Je me pose toujours des question, dois-je calculer
l'aire du parallélogramme pour trouver l'aire de la base?

2. Soit la fonction définie sur [0;10] par: f(x)= x2 (100-x2 a) Etudier les variation de f.
J'ai fais la dérivée de cette fonction et je trouve
j'ai utilisé la formule U'V - UV'
et je trouve 200X, mais le problème c'est de faire le
tableau de variations les ensemble de définition coincident pas... C'est bizarre!

Merci d'avance et désolé pour le dérangement...

[invite44e97bac]

Désolé j'ai pas trouvé "Editer". désolé pour ce triple post.

1. b) Exprimez l'aire du triangle ABC en fonction de x.
J'ai utilisé le théorème de Pythagore dans le triangle ABC pour trouver la hauteur AF (J'ai nommé le point)
Puis j'ai trouvé racine carré de 100 - x²/2
J'ai réduis.

Puis pour l'aire j'ai utilisé la formule B x H / 2
ce qui revient à X fois racine carré de 100 - x2/2 pour la hauteur!
Ensuite, je fais B x H / 2 je trouve donc
x fois racine de 100 - x²/4
Voilà j'ai débloqué ici, merci de me corriger si j'ai tort.

1. c) Exprimez le Volume V du prisme en fonction de X.
Je connais la formule c'est BC x AF / 2 x BE
Donc ce qui revient à X fois racine carré de 100 - x2/2 fois 20
Normalement je dois trouver 5x racine de 100 - x² suivant le logique...

Merci beaucoup d'avance...

Corrigez moi si je me trompe... merci d'avance.