Bonjour,
L'identité d'Euler donne pour la somme infinie de l'inverse des carrés:
zeta2.gif
Est-ce qu'il existe une formule qui donne pour m quelconque le résultat ?
zeta2m.gif
Merci pour vos lumières
-----


Bonjour,
L'identité d'Euler donne pour la somme infinie de l'inverse des carrés:
zeta2.gif
Est-ce qu'il existe une formule qui donne pour m quelconque le résultat ?
zeta2m.gif
Merci pour vos lumières

Malheureusement,
il n'existe pas de formule simple. La somme de la série est trouvée par d'autres moyens qu'exprimer la somme partielle.
Cordialement.


C'est ce que je craignais.
Ca équivaut à trouver une fonction f telle que f(x) - f(x-1) = 1/x². Est-ce qu'on a pu démontrer qu'une telle fonction n'existe pas, ou on a juste pas trouvé ?

Aucune idée !
Mais tu peux chercher ....


Salut,
Finalement j'ai trouvéCa pique les yeux !
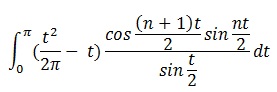

Toujours pas validé. Apparement pour de bonnes raisons.



A l'heure de mon message,ton message (intégrale) n'était pas validé.
Sinon, ta formule est marrante, mais pas très explicite. Remplacer une somme finie par une intégrale qui est une limite de sommes finies pour un nombre de termes qui tend vers l'infini n'est pas parfait.
Mais c'est une jolie formule.Probablement connue depuis longtemps (je en suis pas spécialiste du domaine). Bravo quand même.


Il faut partir de l'égalité
Puis, sommer les intégrales
Oui, je suis d'accord. J'essaie de voir pour une primitive, mais le terme 1/sin n'aide pasRemplacer une somme finie par une intégrale qui est une limite de sommes finies pour un nombre de termes qui tend vers l'infini n'est pas parfait.
Merci, mais je n'ai aucun mérite. L'égalité pour 1/x² n'est pas de moi. Je n'ai pas de démonstration d'ailleursMais c'est une jolie formule.Probablement connue depuis longtemps (je en suis pas spécialiste du domaine). Bravo quand même.

L'égalité doit se prouver par une double intégration par parties, et comme on primitive le cos, puis le sin, on tombe sur 1/k².
Cordialement.


C'est une méthode classique pour calculer zeta (2) : http://gilles.costantini.pagesperso-...iers/zeta2.pdf
voir aussi : http://empslocal.ex.ac.uk/people/sta.../etc/zeta2.pdf

Merci Ericc !


Juste un tout petit peu plus simple en écriture :

Dernière modification par breukin ; 10/12/2012 à 12h31.


Qu'on peut encore améliorer en :





L'intégrateur de Wolfram donne une primitive avec plein de fonctions hypergéométriques....
http://integrals.wolfram.com/index.j...9&random=false
Initilisable en pratique...


La vache ! ça décoiffe

