démonstration du pendule conique

[Leviss]

bonjour à tous,

je suis en train de me préparer pour mes examens en réalisant une série d'exercices de mon syllabus et je viens de tomber sur un problème .

voici mon énoncé :

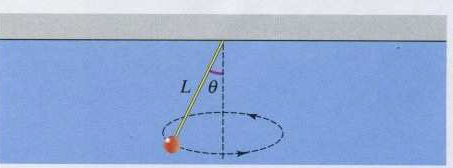
Dans un pendule conique, la masse décrit un cercle horizontal. Montrez que la
période est

T = 2pi * racine ( (L * cos ( α )/g)




Ma résolution :

Sachant que

T * sin α = m v² / R
T * cos α = m*g


mv²/Rsin α = mg/cos α

ce qui me donne

1= mv²*cos α / R sin α g m

1 = v² cos α / R sin α g


où R = sin α * L

1= v² cos α / sin α ² * L*g

1 = v² cos α / (1-cos α ²) * L *g

(1-cos α ² ) * L*g = v² cos α

L*g - L*g *cos α ² = v² cos α


et je suis bloqué ici...


pourriez vous me dire comment je peux démontrer mon problème s'il vous plaît

merci d'avance
-----

[gg0]

Peut-être pas le bon forum ?

[Leviss]

c'est mon professeur de math qui m'a donner cette exercice a faire

[jamo]

Bonjour
que faut il trouver aprés ça : L*g - L*g *cos α ² = v² cos α

[A voir en vidéo sur Futura]

[jamo]

Re
c'est pas une équation diff de second ordre qu'on devrait trouver normalement ?

[gg0]

Quel est le rapport entre T et les variables que tu as utilisées (surtout V et R) ?

Car il s'agit bien d'arriver à T= ..

Cordialement.

[Leviss]

j'ai trouvé sur dans mon livre

T * sin α = m v² / R
T * cos α = m*g

je ne voyais que la subtitution pour parvenir a cela

peut être n'ai je pas les bonne équation...

voulez vous que je poste ce sujet sur le forum de physique pour savoir quoi ?

[gg0]

Comme je ne sais pas d'où sortent les équations que tu utilises, je ne saurais te conseiller. Si c'est un problème de maths, et qu'il faut calculer T à partir des deux formules du début, j'aurais plutôt calculé :

puisqu'il y a une racine carrée dans la formule à trouver, puis réintroduit L dans l'expression. Mais surtout, il y a un lien que tu ne sembles pas utiliser entre la vitesse tangentielle, le rayon du cercle et la période. Une formule où l'angle n'intervient pas (on le réintroduit si on passe de R à L).

Désolé de ne pas être d'une plus grande aide.

[Leviss]

ne vous en faites pas, vous m'avez bien aidé

un grand merci et une bonne soirée

[Leviss]

pour ceux que ça intéresse j'ai la résolution de mon exercice :

Une période est le temps qu'il faut pour se déplacer sur le périmètre à une certaine vitesse.

donc :

X = v*t => t = X/v
X = 2π*R => R = sin α*L
V = √(tg α * g *R)

où X est le périmètre et v la vitesse du mobile

T² = (4π² sin α ² . L ² ) / (tg α * g * R)

T² = (4π² sin α * L ) / (tg α * g)

T = (2π * √( cos a * L )) / g

[jamo]

tout finit bien alors