un peu d'optique, de trigo et de géométrie

[inviteb2d4637e]

Bonjour à tous,

j'espere que vous allez bien. je suis fasse a un petit probleme de math, dans le cadre d'une recherche scientifique.
Meme si la problématiqu est assez complexe, le cas que je vais vous présenter se résume plutot bien et la question semble simple.
J'ai pas mal cherché sans succés, j'espere que l'un d'entre vous aura une idée géniale :




voici le probleme :
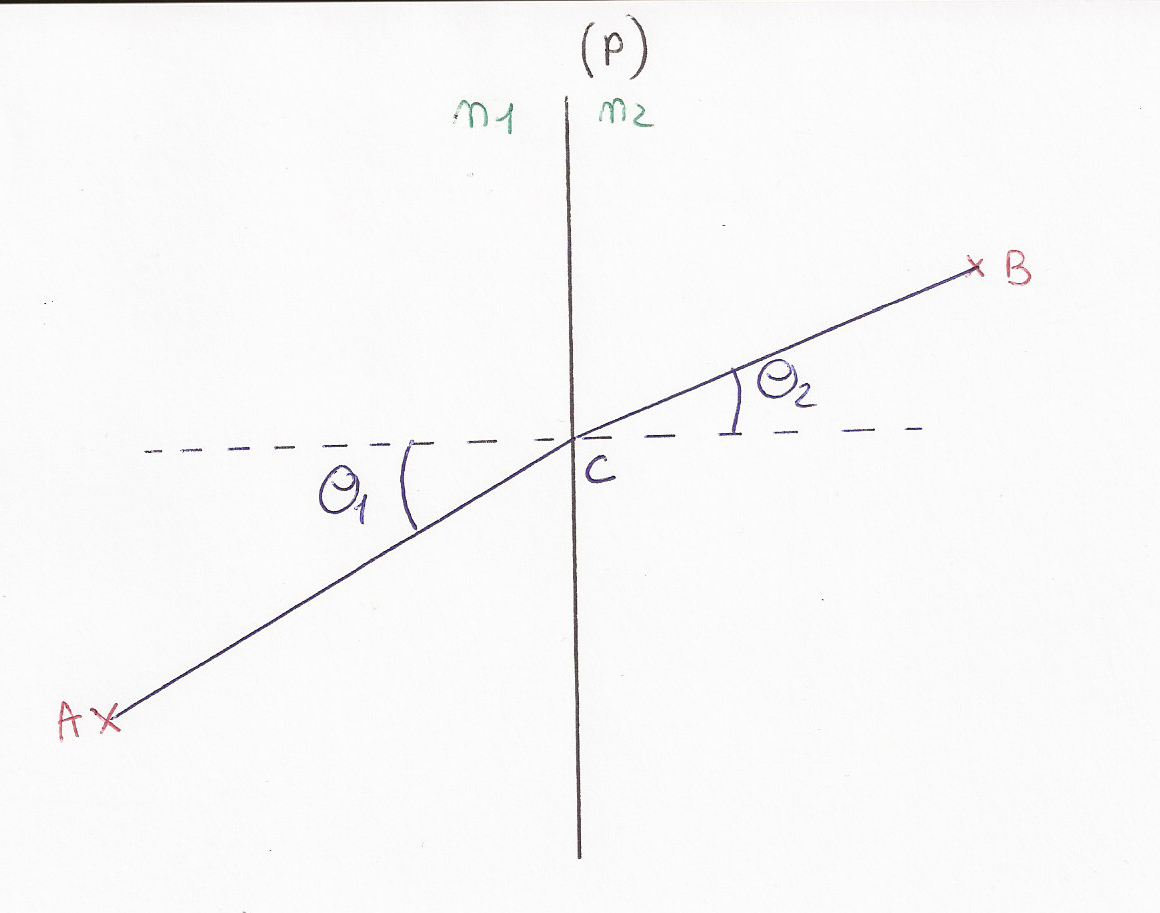
La droite P sépare 2 zones, la première a un indice de réfraction n1 et la seconde un indice n2.
Nous sommes dans un espace cartésien, nous avons les coordonnées des points A,B et de la droite P.

le but du jeu est de connaître les coordonnées du point C, qui est le point d'impact du rayon lumineux qui passe par A et par B.

Descartes nous permet de dire que
n1 x sin(theta1) = n2 x sin(theta2)

Et pour une fois ce n'est pas juste pour la beauté du geste, il y a une application concrète derrière. La droite P est la surface d'un œil et le point B le milieu de la rétine. En pratique il faudra refaire le calcul avec C non pas sur une droite P mais sur un Cercle C (de centre et de rayon connu).

je suis preneur de toute idées, je ne mets volontairement pas les différentes pistes que j'ai pu explorer sans succès pour ne pas vous influencer.

Merci bcp

-----

[inviteb2d4637e]

up?

je suis certain que c'est faisable

[invite8ac20103]

Bonjour,

As-tu essayer par changement de base? i.e. en une base avec C comme origine.

As-tu essayer en résolvant le système d'équation généré par le fais que C est sur la droite de l'intersection du plan P' orthogonale au plan P ( celui de A et B ); de plus C appartient a la droite ( A'B' ) avec A' et B' les projeter orthogonaux de A et B , ( c'est la droite qui sert a définir tes angles ) ?

Cdt

[NicoEnac]

Bonjour,

le but du jeu est de connaître les coordonnées du point C, qui est le point d'impact du rayon lumineux qui passe par A et par B.
...
La droite P est la surface d'un œil et le point B le milieu de la rétine. En pratique il faudra refaire le calcul avec C non pas sur une droite P mais sur un Cercle C (de centre et de rayon connu).

J'ai un problème sur la définition du point B : qu'entendez-vous par "milieu de la rétine" ? Cela signifie-t-il que B est le centre du Cercle C ? Car cela simplifie énormément les choses.
Ne vouliez-vous pas simplement dire "sur la rétine" ?
Pour résumer, nous connaissons : les coordonnées des points A, B et O (centre du cercle C), le rayon du cercle C. Au final, nous cherchons les coordonnées du point "d'impact" du rayon lumineux sur le cercle C. Ai-je bon ?

je ne mets volontairement pas les différentes pistes que j'ai pu explorer sans succès pour ne pas vous influencer.

Ceci n'est pas un site de résolution de problèmes mais d'aide. Donc mettez vos pistes et nous vous aiguillerons.

[A voir en vidéo sur Futura]

[mécano41]

Bonjour à tous,

Si c'est comme j'ai compris (voir croquis) je pense qu'il y a une impossibilité. Il n'y a qu'une position de C (enfin 4 si l'on compte la solution sans intérêt et les symétriques) définie par theta2 et les côtés connus du triangle OBC ; on ne peut donc pas respecter theta 1

Cordialement

[inviteb2d4637e]

Bonjour,

As-tu essayer par changement de base? i.e. en une base avec C comme origine.

As-tu essayer en résolvant le système d'équation généré par le fais que C est sur la droite de l'intersection du plan P' orthogonale au plan P ( celui de A et B ); de plus C appartient a la droite ( A'B' ) avec A' et B' les projeter orthogonaux de A et B , ( c'est la droite qui sert a définir tes angles ) ?

Cdt

Merci pour votre réponse.

j'etais parti sur 3 équations :

n1 sin(theta1) = n2 sin(theta2)
tan(theta1) = CA'/AA'
tan(theta2) = (A'B'-A'C)/BB'

(avec A' et B' les projetés orthogonaux de A et B sur P)

3 équations avec 3 inconnue (theta1, theta2 et A'C).. mais impossible de m'en sortir

[inviteb2d4637e]

Bonjour,

J'ai un problème sur la définition du point B : qu'entendez-vous par "milieu de la rétine" ? Cela signifie-t-il que B est le centre du Cercle C ? Car cela simplifie énormément les choses.
Ne vouliez-vous pas simplement dire "sur la rétine" ?
Pour résumer, nous connaissons : les coordonnées des points A, B et O (centre du cercle C), le rayon du cercle C. Au final, nous cherchons les coordonnées du point "d'impact" du rayon lumineux sur le cercle C. Ai-je bon ?



Ceci n'est pas un site de résolution de problèmes mais d'aide. Donc mettez vos pistes et nous vous aiguillerons.

en fait , j'ai fait un lapsus , il s'agit du milieu de la pupille ( et pas de la rétine, shame on me).donc B est quelque part dans le cerle.. mais pas eu centre du cercle

Pour résumer, nous connaissons : les coordonnées des points A, B et O (centre du cercle C), le rayon du cercle C. Au final, nous cherchons les coordonnées du point "d'impact" du rayon lumineux sur le cercle C. Ai-je bon ?

exactement ca! avec B dans le cercle, le cercle qui contient un liquide d'indice n2 et l'air d 'indice n1...

[inviteb2d4637e]

Bonjour à tous,

Si c'est comme j'ai compris (voir croquis) je pense qu'il y a une impossibilité. Il n'y a qu'une position de C (enfin 4 si l'on compte la solution sans intérêt et les symétriques) définie par theta2 et les côtés connus du triangle OBC ; on ne peut donc pas respecter theta 1

Cordialement

merci pour votre réponse.

J'ai regardé le croquis, il semble bon, est-ce pour simplifier les calcul que vous avez défini yb=0 ?
En pratique (mais pas sur que cela change quelque chose a vos calculs) xb=0 et yb= 2/3R (environ), cela remet il en cause votre réponse?


Merci encore.

[mécano41]

Bonjour à tous,

...J'ai regardé le croquis, il semble bon, est-ce pour simplifier les calcul que vous avez défini yb=0 ?

Non, c'est juste parce que j'avais interprété tes données ainsi...

...En pratique (mais pas sur que cela change quelque chose a vos calculs) xb=0 et yb= 2/3R (environ), cela remet il en cause votre réponse?...

Non. Il te suffit de placer le point B en (0 ; 0,666.R) ou de déplacer le point C de +90° et tu verras que le problème reste le même : 1 seul point C (enfin 4 ....) correspond à un theta2 connu donc : ta relation entre les deux angles ne peut être obtenue...mais peut-être ai-je manqué quelque chose...

Cordialement

[inviteb2d4637e]

Merci mécano41 , je vais réfléchir à tout ca.

[albanxiii]

Bonjour,

Nous sommes dans un espace cartésien, nous avons les coordonnées des points A,B et de la droite P.

le but du jeu est de connaître les coordonnées du point C, qui est le point d'impact du rayon lumineux qui passe par A et par B.

Vous n'avez besoin que du point A et de l'angle d'incidence sur la surface. Cela impose le point C, puis la loi de la réfraction impose l'angle du rayon réfracté et donc le point B.

@+

[inviteb2d4637e]

Bonjour,



Vous n'avez besoin que du point A et de l'angle d'incidence sur la surface. Cela impose le point C, puis la loi de la réfraction impose l'angle du rayon réfracté et donc le point B.

@+

certe, mais je n'ai pas l'angle d'incidence. je sais que le rayon lumineux part de quelque part (A) , qu'il arrive quelque part (B) et qu'il passe par la surface de l'oeil (le point C)
Si n1=n2 je dois avoir C sur [AB]