Math ou physique mathématique ?

[invite67f06a6e]

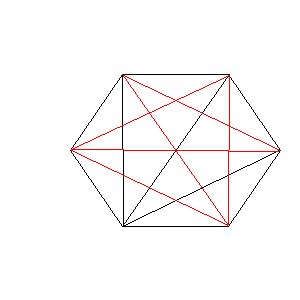
Mon problème est assez simple à expliquer.. Mon fils construit sa maison et je dois faire ses escaliers intérieurs. Je lui ai demandé de me donner les dimensions de la trémie pour que je puisse faire un plan précis. Il m’a envoyé un schéma rapide avec les mesures qu’il a faites. La trémie est un polygone à six cotés et il me donne les mesures prises à partir de chaque angle. Ce qui fait : 6 x 5 /2 = 15 mesures. Je pense que le problème a 9 inconnues car tout hexagone peut être entièrement défini par 4 triangles et ils ont 3 cotés communs. (4x3-3).. Il y a donc redondance des mesures par rapport aux inconnues. Je voudrais employer au mieux cette redondance pour améliorer la précision sur la détermination de la valeur des inconnues. J'ai essayé par les angles et par les équations d'addition qui lient ces angles mais je n'arrive à rien .Comment faire ?
Merci à celui ou ceux qui voudraient me conseiller ou m’aider !
-----

[RoBeRTo-BeNDeR]

Bonjour, je pense que pour pouvoir aider tout ceux qui souhaitent te venir en aide, une figure pourrait être utile.

[invite67f06a6e]

Merci à toi. Je m'empresse de satisfaire ta demande. Je ne suis pas resté inactif depuis mon premier envoi et je pense avoir trouvé une solution sur la méthode. Ce ne sera peut-être ni la seule ni la meilleure aussi je dois faire les calculs avant de vous la soumettre.
Cordialement

[invite67f06a6e]

J'ai l'impression que la photo n'est pas passée. C'est un.fichier bmp de 2.55Mo .Je cherche une solution

[A voir en vidéo sur Futura]

[invite67f06a6e]

Je renonce à réussir ce soir à la fois un dessin lisible, de petite taille informatique, avec la bonne extension etc.
Nous allons donc faire autrement :
La France est, dit-on souvent, hexagonale. tout le monde voit je pense
Choisissons 6 villes à la périphérie géographique : Strasbourg, Lille, Brest, Saint Jean de Luz, Montpellier et Nice par exemple. Supposons que nous ayons mesuré les distances séparant ces villes plus ou moins précisément... Et bien nous venons de décrire mon problème sans dessin ! Il y a 15 mesures de distance entre ces villes et nous n'avons strictement besoin que d'en connaitre 9 pour tracer un hexagone. Comment faire pour tracer la meilleure carte en utilisant toutes les données ?
J'espère que pour une fois un long discours est aussi clair qu'un petit dessin....

[Médiat]

Si j'ai bien compris votre problème, voilà le dessin (l'hexagone pourrait être moins régulier) :

En noir 9 mesures "suffisantes", en rouge, 6 mesures redondantes pour améliorer la précision.

[Bruno]

Bonjour,

En fait un polygône est entièrement défini par son centre (2 paramètres), son rayon et son orientation, soit 4 paramètres. Comme ici seules les dimensions importent et non la position absolue, le problème se réduit à l'estimation du rayon r.

- La distance entre 2 cotés adjacents est: y = 2rsin(30°) (6 relations de ce type)

- La distance entre 2 cotés opposés est: y = 2rsin(90°) = 2r (3 équations)

- La distance entre 2 cotés pris 1 sur 2 est: y = 2rsin(30°) (6 équations)

Il suffit alors d'écrire tout ça sous forme de matrices colonnes: [ y ] = A*r et tout ce qu'on peut faire à ce stade c'est une estimation par moindres carrés : r = (A^T*A)^{-1}*A^T*y

Problème 1: cette méthode donne de bons résultats si le bruit de mesure est "aléatoire" de moyenne nulle (une erreur systématique de mesure casse tout, mais est rattrapable en ajoutant un paramètre à estimer).

Problème 2: rien ne nous dit que ce qu'il a mesuré est réellement un hexagone, mais là c'est un problème de modèle.

[Médiat]

Bonjour,

Rien ne dit que l'hexagone est régulier.

[invite67f06a6e]

Je crois me souvenir d'avoir appris " La géométrie est l'art de raisonner juste sur une figure fausse". En effet nous sommes presque dans cette situation : Le texte associé au dessin de notre modérateur spécifie que l'hexagone pourrait être plus irrégulier. Il a raison, le mien est complètement irrégulier ou presque (je dis cela car le maçon ayant fait de gros efforts, il n'est pas impossible que finalement nous lui trouvions un ou deux angles droits). Pour mettre fin à toute mauvaise interprétation, je suis allé me rafraichir les idées chez wiki et j'en tire que le polygone ABCDEF dont nous parlons est un [COLOR="#FF0000"][COLOR="#FF0000"]polygone convexe d'ordre 6. Par ailleurs, les mesures ont été effectuées avec beaucoup de soins et voici les valeurs obtenues : AB=860 ; AC=3585 ; AD=3800 ; AE=2850 ; AF=937 ; BC=2860 ; BD=3196 ; BE=2375 ; BF=1282 ; CD=802 ; CE=1320 ; CF=3237 ; DE=1045 ; DF=3262 ; EF=2235. Ces mesures sont en millimètres et le chiffre des mm n'est pas forcement significatif. Celles et ceux d'entre vous souhaitant se convaincre qu'il est bien irrégulier peuvent soit le tracer eux même soit continuer à suivre notre discussion jusqu'à sa fin...
Je pense avoir tout dit. Si je n'ai pas donné ces valeurs plus tôt c'est que mon problème n'est pas de me décharger du travail de calcul mais de définir une méthode qui, à la réflexion, doit être utilisée par les géomètres.

[Amanuensis]

Annulé, grosse erreur...

[invite179e6258]

sinon, un peu hors sujet : pour ajuster un escalier à une trémie, on n'a pas besoin d'une précision millimétrique, sinon rien ne se ferait jamais dans le bâtiment.

[Bruno]

OK le polynôme est non régulier, mais quel est le but au final ? Avec 12 mesures de distance et Al-Kashi, on peut déjà tracer le polynôme et se servir des 3 mesures restantes pour vérifier si ça colle niveau angles.

[invite67f06a6e]

Non Bruno, il suffit de 9 mesures seulement pour déterminer l'hexagone :
un coté disons AB (une mesure) et à partir des extrémités A et B de ce coté deux mesures pour chacun des sommets restants C,D,E,F donc (1+ 2 x 4) = 9 mesures.
Je suis presque d'accord avec Toothpick-Charlie mais, je dois faire un escalier à limon central courbe et donc sans autre appui que les extrémités. Dans l'espace, en partant du bas je dois arriver là où il faut à l'étage supérieur (c'est la partie plus physique du problème) et tant que faire, autant déterminer la cible le mieux possible, vous ne croyez pas ?
Et puis cela nous force à réfléchir ! C'est cela aussi le plaisir!

[Bruno]

Oui bien sur que 9 mesures suffisent (les 5 côtés + 4 angles), mais les 12 mesures permettent une vérification directe. Ceci dit, je ne vois toujours pas quel est le problème à résoudre, ce serait bien que tu nous l'expliques avant de se lancer dans des estimations d'angles... (et de toute façon 15 mesures pour 9 paramètres, je doute que ce soit assez pour une estimation correcte).

[invite67f06a6e]

Je reviens, Bruno, sur ton message 3675. Quelles sont les 12 mesures dont tu parles? J'ai utiliser les 15 mesures disponibles pour calculer tous les angles de tous les triangles intérieurs à l'hexagone. J'ai un certains nombre de relation entre les angles qui sont du type CAE=CAD+DAE et BAE=BAC+CAD+DAE ou encore BAF=BAC+CAD+DAE+EAF. Je sais aussi la somme des angles d'un hexagone convexe (ABCDEF) fait 720 degrés, que celle des angles d'un pentagone convexe (p.e.ABCDE) fait 540 degrés, que celle d'un quadrilatère (p.e. ABCD) fait 360 degrés et que celle d'un triangle (p.e. ABC) fait 180 degrés. Mais qu'est ce que j'en fais ? ou cela me mène-t-il ? C'est là que j'ai buté avec les angles! Je trouve un peu facile de répondre à quoi cela sert-il? Nous sommes ici dans un forum de mathématiques ! non ?

[invite67f06a6e]

Il me paraît important de revenir vous parler de mon "polygone d'ordre 6 convexe et irrégulier: A,B,C,D,E,F" voilà ce que j'ai fait pour essayer de tirer partie des données excédentaires dans mon problème.
(1) A partir de chaque côté, j'ai déterminé les positions des 4 sommets qui leur font face. J'ai donc obtenu six hexagones entièrement définis.
(2) Pour chacun de ces hexagones, j'ai calculé les quatre angles BAC, CAD, DAE et EAF ainsi que les cinq longueurs AB, AC, AD, AE et AF. Ensemble elles définissent un hexagone.
(3) Ayant ainsi six déterminations de chacune de ces quantités , j'ai fait la moyenne pour chacune d'elles et ai considéré que ces moyennes me donnaient l'hexagone le plus probable !
Je ne sais pas justifier le processus que je viens de décrire autrement que par des considérations d'ordre générales :
- Je pense que les mesures "excédentaires" contiennent la même "quantité d'information" que les autres et qu'on ne peut que gagner à les prendre en compte.
- J'ai pris soin de faire jouer le même rôle à chacune des mesures de la même catégorie : celle des côtés et celle des diagonales.
C'est, je pense la symétrie du traitement qui soutient le mieux la méthode.
Je serais très heureux de recevoir vos commentaires, fussent-ils négatifs !
Merci à tous.