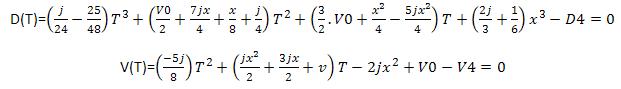Vitesse maximale entre deux points

[invited6d2f678]

Bonjour,

Depuis hier, j'essaie de trouver une solution à un problème qui me paraît pourtant plutôt simple mais je n'arrive pas à m'en sortir.
Je vais prendre l’exemple avec une voiture pour que le problème soit plus imagé.

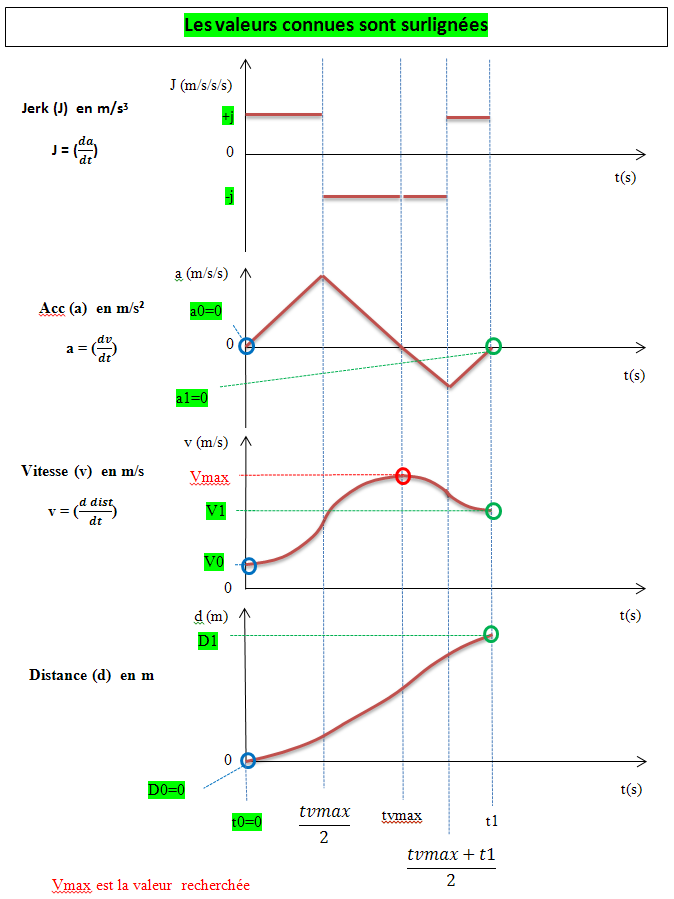
Tout d'abord la voiture est au point 0 avec les caractéristiques suivantes:
t0=0s, d0=0m, v0=variable connue en m/s, a0=0m/s² et le jerk noté j0=variable connue en m/s3

Je sais que la voiture doit être au point 1 avec les caractéristique suivantes:
t1=inconnue, d1=variable connue en m, v1=variable connue en m/s, a1=0m/s² et j1=j0=variable connue en m/s3

Sachant que la vitesse v1 au point 1 est forcement atteignable par la voiture depuis la vitesse v0 au point 0.

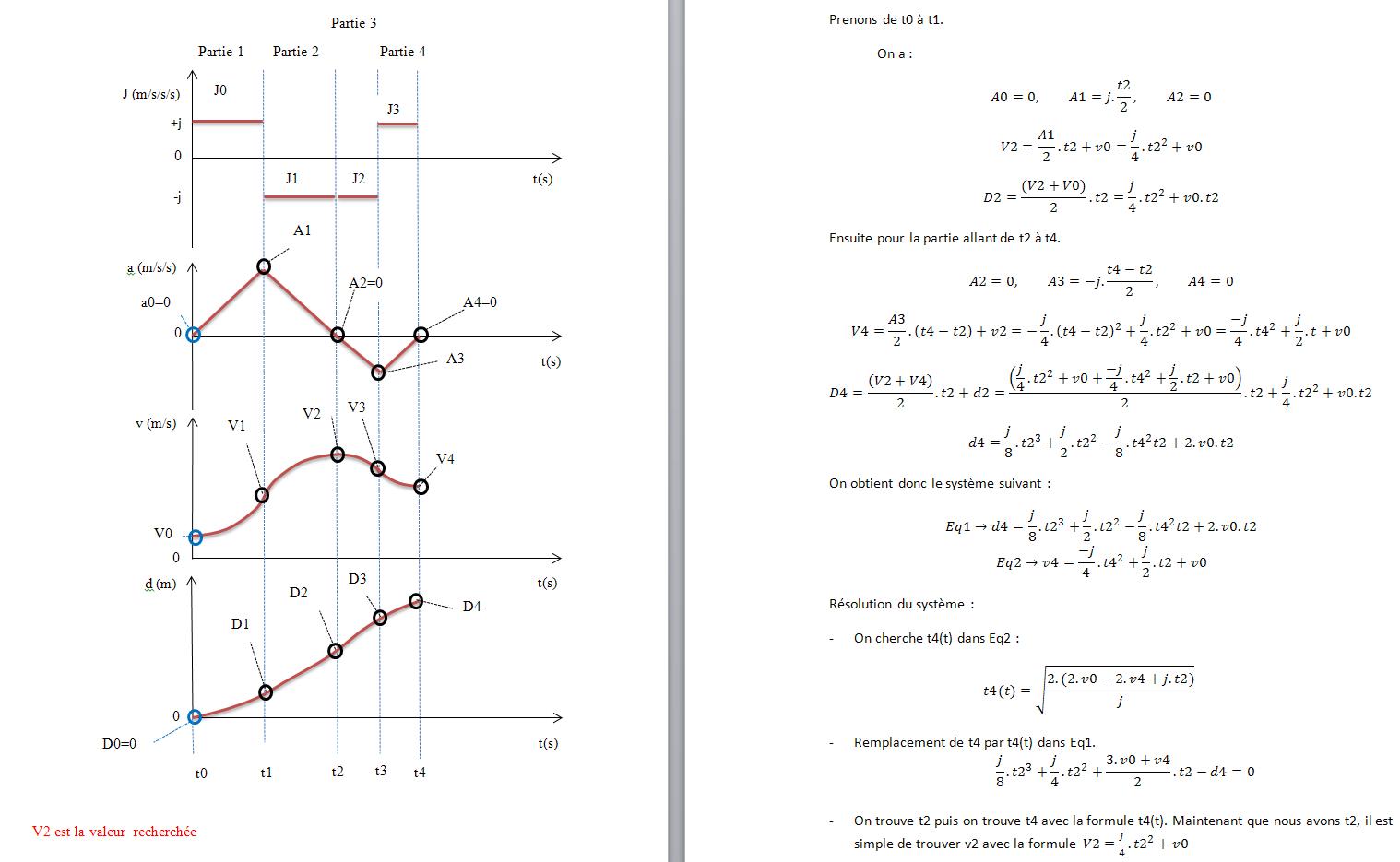
Avec ces données, je recherche la vitesse maximale atteignable par la voiture entre ces deux points tout en respectant leurs caractéristiques.

Vmax (t0,d0,v0,a0,j0,d1,v1,a1,j1)?

J'ai fait des tonnes calculs dans tous les sens mais je tourne vraiment en rond.

Merci pour votre aide.
-----

[gg0]

Bonjour.

Il n'y a aucune raison de pouvoir traiter ce problème si tu n'as pas une relation entre les variables. Autre que les définitions de la vitesse comme dérivée de la position et de l'accélération comme dérivée de la vitesse (ce que tu appelles le jerk -pour moi c'est une danse des années 60-70 - c'est la dérivée de l'accélération ?), dérivées par rapport au temps.
Dans un problème de dynamique, il y a ce type de relations, qui permettent d'avoir une équation différentielle ou un système différentiel.

Cordialement.

[albanxiii]

Bonjour,

(ce que tu appelles le jerk -pour moi c'est une danse des années 60-70 - c'est la dérivée de l'accélération ?), dérivées par rapport au temps.

Oui.

@+

[invited6d2f678]

Bonjour,

Désolé pour le temps de réponse. Ci-joint l'explication de mon problème.




Merci.

[A voir en vidéo sur Futura]

[inviteea028771]

Le problème c'est qu'il y a une infinité de courbes qui coïncident sur les valeurs que tu connais. On peut choisir une Vmax arbitraire, et construire une courbe qui colle a tes données

[gg0]

Ok, mais on est loin de ton énoncé du début !

Si je comprends bien, tu cherches à caler les valeurs t2,t3 (ce que tu appelles tvmax) et t4 pour que t2=t3/2 et t4=(t1+t3)/2, que la vitesse soit maximale en T3 et que le "jerk" soit à j de 0 à t2, égal à -j de t2 à t4, puis à nouveau à j de t4 à t1, et que la distance parcourue soit D1 au bout du temps t1.
Es-tu sûr que c'est possible ?
Les conditions sur t2, t3 et t4 font qu'on doit déterminer une seule variable (t3) avec deux équations : la valeur V1 - V0 (le V0 est une constante additive dans les équations de vitesse) et la valeur D1.
A priori, sauf choix adapté de V0, V1 et D1, le problème n'aura pas de solution.

Cordialement.

[invited6d2f678]

Effectivement la formule pourrait ne pas avoir de solution, mais tout ce calcul intervient dans une routine ou on s'assure en amont que la vitesse V1 au point 1 soit accessible depuis la vitesse V0 au point 0 (Les deux points étant distants d'une distance connue).

Cordialement.

[gg0]

Alors la vitesse V1 ne fait pas partie des données !

Avec seulement D1 comme contrainte, ça devrait pouvoir aller. Il suffit d'écrire les fonctions accélération, vitesse et position en fonction de t et du paramètre t3, puis de résoudre l'équation d(t1)=D1 d'inconnue t3. Qui devrait être de degré 3 en t3, ce qui peut poser un problème car il n'existe pas toujours d'expression algébrique des solutions d'une équation du second degré (mais des méthodes trigonométriques).
Le calcul est assez pénible, je ne suis pas motivé pour le faire, mais est seulement long. On exprime successivement chacune des fonctions sur chaque intervalle. Si tu peux te faire aider d'un calculateur formel (Mathématica, Maple, Wims, ou autre), ce sera plus facile et avec moins d'erreurs.

Si la vitesse V1 est donnée, et seulement vérifiée comme possible, je ne garantis rien. t3 est déterminé en fonction de V0 et V1, rien ne garantit alors que la distance parcourue (qui n'a plus de paramètre pour la faire varier) soit bien D1.

Cordialement.

[invited6d2f678]

Merci beaucoup pour vos réponses et de vous intéresser à mon problème.

En faite les deux contraintes sont nécessaires. Il faut trouver, en une distance donnée, avec une vitesse donnée au début de cette distance et une vitesse donnée en fin de cette distance, la vitesse maximale atteignable.

Pour résoudre ce problème, je m'y suis pris de la façon suivante.

Je renomme les phases de la façon suivante afin que ma démarche soit plus compréhensive:
- la phase 1 la phase accélération positive + jerk positif. (elle va du point 0 au point 1)
- la phase 2 la phase accélération positive + jerk négatif.(elle va du point 1 au point 2)
- la phase 3 la phase accélération négative + jerk positif.(elle va du point 2 au point 3)
- la phase 4 la phase accélération négative + jerk positif.(elle va du point 3 au point 4)

On cherche donc la vitesse V2.
J'ai regrouper les phases 1 et 2 dans une seule même formule de dynamique et j'ai fais de même chose pour les phase 2 et 3.
Une fois ces deux formules crées, je recherche la donnée respectant les contraintes suivante.
- la distance parcourue par les deux deux formules (une fois additionnées) doit être égal à la distance imposé (d4).
- la vitesse doit être la même pour les deux courbes.

Enfin bref... Je peu vous envoyer les calculs si ça vous intéresse.

Mais à la fin j'arrive à ce système que je n'arrive pas à résoudre.
ay³+by+ax³+cy+d=0
et
ey²+b=fx²+c

ou seul x et y sont inconnues. Le reste est des constantes.

Et là je n'y arrive pas. Est-ce possible de résoudre ce système.

Merci.

Cordialement.

[gg0]

Je ne comprends pas bien le rapport entre ce que tu dis maintenant et le schéma du message #4. N'importe comment, le jerk déterminer l'accélération, la vitesse (compte tenu de V0) et la position. J'ai cru comprendre ce que tu voulais faire, mais tu ne réponds pas à mes questions. Si tu fais autre chose que ce que je crois, comment savoir, ou même interpréter tes éventuels calculs
Ton système a des solutions, qu'il est sans doute malaisé de déterminer algébriquement. et rien ne dit qu'il en a dans le bon intervalle !

Bon, je te laisse, car c'est inutile de continuer si on ne sait pas quelle est la vraie question.

Cordialement.

[invited6d2f678]

Désolé pour mon explication un peu vaseuse.

Voici ma démarche détaillée. Si il y a un problème de calcul ou de compréhension sur mes explications, n’hésitez à ma poser une question.

Determination vitesse max 2x.pdf

Merci beaucoup de m'aider.

[gg0]

Bonjour.

j'ai essayé de comprendre, mais tu mélanges allègrement les variables et les constantes (ce qui doit te simplifier le calcul, mais le rend faux). Par exemple la formule 1 ne concerne pas t mais t₁. Sans compter avec les changements de variables qui faussent les équations (dériver par rapport à t ne donne pas le même effet que dériver par rapport à x - formule de dérivation des fonctions composées). Donc des calculs apparemment faux (le j/8 t³ me paraît bizarre).
Autre chose : dans ton message d'hier, il y avait des contraintes sur les temps qui ne sont plus présentes ici. Ce sont elles qui me faisaient dire qu'il n'y a probablement pas de solution.

Il serait bien que tu explicites vraiment, pas sur un schéma où on ne sait pas ce qui est hypothèses et conséquences, quelle est la question que tu veux traiter. Pour l'instant, je ne sais toujours pas.

Cordialement.

[invited6d2f678]

Dans la formule 1, le t dois être égal à t2 mais cette équation et l'équation de mouvement de ma première phase mais effectivement il y a des erreurs avec le changement de variable.

Je vais essayer de poser ma question le plus simplement possible.

Je suis à un point avec une vitesse donnée par (exemple 5m/s) avec une accélération nulle.
Je sais que dans une distance donnée (par exemple 100 m) je devrais être à une vitesse donnée (par exemple 15 m/s) avec une accélération nulle.
Entre ces deux points, je n'ai aucune limite de vitesse mais seulement le coefficient de Jerk (par exemple 10 m/s³).

Quelle est la vitesse maximal que je pourrait atteindre?

Voilà, je pense que c'est plus compréhensible?? Enfin je crois??

Cordialement

[gg0]

Continuons à préciser :

Le coefficient de Jerk est-il constant ? ou bien doit-il être constant par intervalle ? Ou encore, doit-il être constant positif égal à j sur un intervalle puis constant négatif égal à -j sur un autre ? Ou bien comme sur le schéma ?
A chacun de ces problèmes, il y a une réponse différente sur la vitesse maximale. Il est évident que même avec des Jerk constants mais quelconques, on peut atteindre (en théorie) des vitesse aussi grandes qu'on veut. Idem avec le Jerk variable.

Donc continue à préciser complétement ton problème ...

[invited6d2f678]

Au niveau du Jerk:

Pour continuer sur l'exemple donner,
Point 0:
je suis au point 0 à V0=5m/s à t0=0s et à d=0m avec une accélération nulle (a0=0m/s2), le Jerk passe alors à la valeur donnée en positif (exemple j=10 m/s3). Le jerk reste constant et positif jusqu'au point 1.

Point 1:
Le jerk passe alors en négatif (j=-10m/s3). Il reste constant jusqu'au point 2.

Point 2:
On atteint ici la vitesse maximal où l'accélération doit être nulle. le jerk reste négatif et constant.

Point 3:
Le jerk passe alors en positif (j=10m/s3). Il reste constant jusqu'au point 4.

Point 4:
Arrivée au point 4 à avec une accélération nulle, une vitesse égale à la vitesse données (exemple V4=15m/s) et la distance égale à la distance voulue (d4=100m).

Cordialement

[gg0]

Ok.

On est donc dans le cadre de ton deuxième dessin. le plus simple alors est de déterminer les fonctions accélération, vitesse et position en fonction des contraintes, avec comme variables t₁=x et t3=y, les temps d'arrivée aux points 1 et 2. J'ai pris x et y car les indices sont pénibles à écrire. La valeur de t₂=m se déduira des autres. je note aussi t₄=T.
On commence par définir la fonction accélération, qui vaut :
a(t)=jt pour 0<=t<x
a(t)=j(2x-t) pour x<=t<y
a(t)=j(t+2x-2y) pour y<=t<=T

"Arrivée au point 4 à avec une accélération nulle,.." donc j(T+2x-2y)=0 ce qui donne y=x+T/2.
Il ne reste plus qu'une seule variable à déterminer. On en déduit aussi que j(t+2x-2y)=j(t-T)

Ensuite, on passe à la vitesse, en intégrant :
v(t)=jt²/2+V0 pour 0<=t<x
v(t)=j(2xt-t²/2)+C1 pour x<=t<y
v(t)=j(t²/2-Tt)+C2 pour y<=t<=T
Et on détermine C1 et C2 pour que les valeurs en x et y concordent : C1=V0-jx² et C2=V0+j[Ty-(x²+y²-2xy)] = V0+j[T(x+T/2)-(T/2)²] = V0+jT(x+T²/4).

"Arrivée au point 4 à avec une accélération nulle, une vitesse égale à la vitesse données (exemple V4=15m/s)" On pose v(T)=V4, ce qui donne la valeur de x :

Ce qui permet de trouver la valeur où la vitesse est maximale en cherchant a(t)=0 sur l'intervalle [x,y].
Mais, car il y a un mais, il reste une condition :
"Arrivée au point 4 avec ... la distance égale à la distance voulue (d4=100m)"
Or on n'a plus de variable à changer ! Et sauf immense hasard, il n'y a aucune raison que la distance parcourue en tenant compte de la fonction vitesse permette de parcourir exactement la distance prévue.

Conclusion : Ton problème n'a pas de solution.

Cordialement.

[invited6d2f678]

C'est bon, je viens de résoudre mon problème.



Merci de m'avoir aidé et désolé pour mes explications.

[invited6d2f678]

Merci gg0, je suis parti sur une autre direction et je retombe bien sur une réponse.
J’essaie de comprendre mais je ne vois pas où tu trouves la valeur de T.

Merci beaucoup de ton aide gg0.

[gg0]

T n'est pas une constante ?
Dans ce cas, alors on peut effectivement déterminer x et T par les deux dernières conditions. Et trouver quelle est la vitesse maximale.

Cordialement.

[invited6d2f678]

Super!!! Merci beaucoup de ton aide.

Cordialement.

[invited6d2f678]

Bonjour gg0,

j'ai chercher à utiliser votre méthode (car la mienne doit être fausse) pour résoudre le probléme mais je retombe à la fin sur un système impossible à résoudre.

J'ai repris exactement votre système de notation.

On est donc dans le cadre de ton deuxième dessin. le plus simple alors est de déterminer les fonctions accélération, vitesse et position en fonction des contraintes, avec comme variables t₁=x et t3=y, les temps d'arrivée aux points 1 et 2. J'ai pris x et y car les indices sont pénibles à écrire. La valeur de t₂=m se déduira des autres. je note aussi t₄=T.
On commence par définir la fonction accélération, qui vaut :
a(t)=jt pour 0<=t<x
a(t)=j(2x-t) pour x<=t<y
a(t)=j(t+2x-2y) pour y<=t<=T

Sur la dernière équation pour y<=t<=T, a(t)=jx-jx-jy+j(t-y-2x)=j(t-2x-2y)

donc j(T+2x-2y)=0 ce qui donne y=x+T/2.
Il ne reste plus qu'une seule variable à déterminer. On en déduit aussi que j(t+2x-2y)=j(t-T)

Du coup, on obtient ici j(T-2x-2y)=0 ce qui donne y=T/2-x et par conséquent j(t-2x-2y)=j(t-T) se qui semble graphiquement bon.

Maintenant que nous avons les formules d'accélérations des trois parties, j'ai fais comme vous, j'en ai déduit les vitesses.
Une fois les formules de vitesse déduit pour chacune des phases, je me place alors à l'instant T, évidement avec la formule v(t) pour y<=t<=T.
Je calcul donc V(T), je remplace les composantes y par x+T/2 et bien sûr t par T.

Je sais que v(T)=V4, j'ai ici m'a première équation avec deux inconnues (x et T).

Ensuite j'en déduit, en dérivant les équations de vitesse des trois phases, les formules de distance parcourue d(t).
Une fois les formules de distance déduit pour chacune des phases, je me place alors à l'instant T, avec la formule d(t) pour y<=t<=T.
Je calcul alors d(T), je remplace comme précédemment les composantes y par x+T/2 et toujours et bien sûr t par T.

Je sais que v(T)=D4, j'ai ici m'a seconde équation avec deux inconnues (x et T).

Mais seulement voilà, le système est très compliqué.



Voyez une autre solution pour s'affranchir de la résolution de ce systéme?

Merci.

Cordialement.

[gg0]

Bonjour.

Il n'y a aucune raison pour que le système ne soit pas compliqué : les contraintes sont fortes et multiples. C'est déjà bien que les contraintes permettent d'avoir un système (et peut-être des solutions). le mieux serait d'essayer de voir si un logiciel formel (Mathématica, Maple, Wims, ...) permet de résoudre. Wims est en ligne mais délicat à utiliser, Maxima et Xcas sont librement téléchargeables.
Si j'ai le temps, je regarderai avec ma vieille version de Maple.

Cordialement.

[invited6d2f678]

Merci beaucoup.

Je vais essayer de les télécharger. A la main je ne m'en sort pas.

Merci.

[invited6d2f678]

Je viens d'essayer une autre méthode qui me semble plus simple en calcul.

Le système reste tout de même compliqué.


Cordialement

[invited6d2f678]

a la fin de la dernière équation c'est (3/2)*w*y

[gg0]

Voila,

j'ai regardé ce que donne le système que tu proposais ce matin (je regarderai ta nouvelle proposition quand ce sera possible, que le fichier aura été validé). Il y a une lettre parasite dans la deuxième équation, un v. Maple trouve que x est solution d'une équation très compliquée de degré 9 (même avec des valeurs numériques : ( pour tes données avec v=0 car je ne sais pas ce que c'est). Il ne la résout pas, pour cause !

Et le calcul approché ne donne rien ! pas de convergence pour un calcul direct; des solutions complexes non réelles comme valeurs approchées des solutions exactes. A noter : L'équation ci dessus semble ne pas avoir de solution positive. Mais le v a sans doute une valeur non nulle.

Cordialement.

[gg0]

Je viens de regarder ton nouveau document, je ne vois aps le rapport avec le problème que tu posais !

Désolé !

NB : je vais te laisser faire, car tu es lancé dans une problème dont je ne vois pas l'intérêt d'y consacrer plus de temps. Surtout si l'énoncé change !

[invited6d2f678]

- L'énoncé ne change pas, c'est juste une autre méthode, qui au lieu de calculer toute la trajectoire et d'obtenir un système au niveau de la fin de la trajectoire,permet de partir des deux extrémités (deux vitesse que l'on connaît, espacé d'une distance connue) pour obtenir un système au niveau de la vitesse maximal, c'est tout. Les deux méthodes réponde exactement au même problème qui est exactement le même depuis le début de la discussion. Mon problème est un problème réelle pour une application réelle.

- Je suis entrain d'essayer sur maxima avec la première et la seconde méthode. Mais il n'arrive pas à résoudre. Je ne comprend, pourtant si on le fait graphiquement, il y a bien des solutions, alors pourquoi est-ce impossible par calcul??

Cordialement.

[gg0]

1) Ce n'est plus le même problème vu l'utilisation de x/2. Tu reviens à ta formulation initiale qui rendait le problème impossible.
2) Ce n'est pas parce qu'un calcul est posé qu'on sait le résoudre. on a même prouvé des impossibilités de faire certains calculs (résolutions algébriques d'équations, calcul effectifs de primitives). Ce que tu appelles résolution graphique est un travail approché. Si tu veux une résolution approchée, utilise un logiciel qui fait du calcul scientifique approché, Scilab, par exemple qui est gratuit.

Cordialement.

[invited6d2f678]

J'ai fais le système comme vous me l'avez conseillé sur wxMaxima, je joins le fichier.

Test4.zip

Le système est en faite une peut plus simple mais le logiciel n'arrive toujours pas à le calculer.

Cordialement.