origine des structures algébriques

[exponontielle]

Bonjour,
on parle de structures algébriques comme étant une nouvelle théorie qui vient de substituer la théorie des ensembles.on définit des structures tq ;le groupe, corps,anneau...par un ensemble d'axiomes que doit vérifier les lois de composition.
ma question est:c'est quoi ce catalyseur qui a poussé les savants à en penser ?pourquoi ils ont cherché une tel théorie ?.
merci d'avance.
-----

[PlaneteF]

Bonjour,

Pour être précis, tu ne voudrais pas plutôt parler de la théorie des catégories ?!


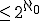Cordialement

[Seirios]

Bonjour,

Les structures algébriques sont définies sur des ensembles, donc la théorie des ensembles reste antérieure. Pour ce qui est de justifier l'introduction des structures algébriques, je pense qu'on peut dire que les mathématiciens ont cherché à reconnaître les quelques structures qui apparaissent la plupart du temps et d'en montrer les propriétés principales pour éviter de les remontrer dans chaque cas particulier.

[exponontielle]

merci bcp Seirios pour ta réponse,mais je pense que la réponse est plus profonde ,parce que pour un même ensemble on peut définir plusieurs structures (par exemple l'ensemble R des réels il est un groupe,corps à la fois).cette multitude des structures reste un énigme mais qui a un réponse dans un contexte historique ,comment ABEL a pensé du structure du groupe pour décrire des permutations des racines d'une équation algébrique(comme j'ai lu dans un article )??

[A voir en vidéo sur Futura]

[Médiat]

Bonjour,

La théorie des groupes est due à E. Galois, elle lui a même certainement couté la vie. Galois s'est inspiré des travaux de Lagrange sur les équations polynomiales.

D'autre part, IR est beaucoup plus que ce que vous en dites, un isomorphisme entre ensembles non munis de structure est simplement une bijection, ce qui d'ailleurs définit la notion de cardinal, c'est à dire que, d'une certaine façon, un ensemble sans structure, n'est rien d'autre qu'un "nombre d'éléments". IR peut-être muni de toutes les structures axiomatisées au premier ordre dans un langage de cardinal .

[taladris]

par exemple l'ensemble R des réels il est un groupe,corps à la fois

Difficile d'etre corps sans etre groupe.

[Seirios]

merci bcp Seirios pour ta réponse,mais je pense que la réponse est plus profonde ,parce que pour un même ensemble on peut définir plusieurs structures (par exemple l'ensemble R des réels il est un groupe,corps à la fois).cette multitude des structures reste un énigme mais qui a un réponse dans un contexte historique ,comment ABEL a pensé du structure du groupe pour décrire des permutations des racines d'une équation algébrique(comme j'ai lu dans un article )??

Intrinsèquement, il n'y a qu'une seule structure ; la multitude (si elle est réelle, cf. la remarque de taladris) vient simplement du fait que l'on a donné des noms à des structures et pas à d'autres. Après, il y a plusieurs approches possibles de la structure que l'on étudie, ce qui nous donne différents points de vue.

[Médiat]

Intrinsèquement, il n'y a qu'une seule structure.

On peut munir IR d'une structure de corps non commutatif, c'est quand même différent de sa structure habituelle, non ?

[PlaneteF]

La théorie des groupes est due à E. Galois, elle lui a même certainement couté la vie.

Bonjour Médiat,

L'histoire que l'on peut lire partout (dont Wikipédia) raconte une mort suite à un duel, pour les beaux yeux d'une demoiselle parmi les raisons évoquées de ce duel.

Du coup je ne comprends pas le sens de ta phrase ?


Cordialement

[Médiat]

Bonjour

L'histoire que l'on peut lire partout (dont Wikipédia) raconte une mort suite à un duel, pour les beaux yeux d'une demoiselle parmi les raisons évoquées de ce duel.

Et il a passé la nuit avant le duel à rédiger son "testament mathématique", il avait donc fort peu dormi, et n'était pas au mieux de sa forme pour participer à un duel (s'il avait été en pleine forme il serait peut-être mort quand même, mais il aurait eu plus de chances de s'en sortir).

[Seirios]

On peut munir IR d'une structure de corps non commutatif, c'est quand même différent de sa structure habituelle, non ?

J'ai considéré que les opérations étaient fixées (sinon, on peut dire à peu près n'importe quoi).

[Médiat]

(sinon, on peut dire à peu près n'importe quoi).

Disons que l'on peut tout dire, c'est bien le sens de ma première intervention.

[Amanuensis]

Question: Y a-t-il des cas où la description d'une structure ne peut pas se ramener à une liste d'ensembles? (Comme par exemple un espace topologique est la donnée d'un ensemble et d'un sous-ensemble de ses parties respectant quelques propriétés, ou un groupe est la donnée d'un ensemble et d'un sous-ensemble de ses permutations respectant quelques propriétés.)

[Médiat]

Réponse : dans la mesure ou les constantes d'un langage forment un sous-ensemble d'un certain ensemble M, que les relations sont des sous-ensembles de Mⁿ, et que les fonctions ne sont que des relations particulières, la réponse est donc oui, pour toute la logique classique du premier ordre (bien que je n'en soit pas spécialiste, cela doit aussi être vrai pour les logiques d'ordre supérieur (j'ai un léger doute sur les axiomes utilisant des quantifications sur les formules), et pour les logiques modales qui peuvent se décrire par des modèles de Kripke).

[exponontielle]

merci à vous tous,pour vos interventions

[exponontielle]

les structures axiomatisées au premier ordre dans un langage de cardinal .

j'ai pas compris ce que vous voulez dire M.Médiat

[Médiat]

Si un langage est de cardinal il est possible que ne puisse pas interpréter tout le langage dans un ensemble de cardinal comme , par exemple si les axiomes exigent d'avoir plus de constantes différentes que le cardinal de .

Vous pouvez laisser tomber ce détail, je ne l'ai ajouté que parce que je n'aurais pas aimé écrire quelque chose que je savais faux.

[exponontielle]

non j'ai pas compris d'abord c'est quoi un langage de cardinal??

[Médiat]

Visiblement vous n'avez pas de connaissances approfondies en logique, et continuer sur ce terrain pourrait vous entraîner trop loin, sans rien vous apporter, sachez seulement que si une axiomatique exige plus d'éléments différents que IR n'en a, IR ne pourra pas être une structure de cette axiomatique (un ensemble à 2 éléments ne peut pas être une structure pour une axiomatique qui en exige 3, c'est le même principe).

[martini_bird]

Bonjour,

pour répondre à la question initiale, et si l'on considère les structures algébriques du point de vue axiomatique et formel, alors la paternité revient sans doute à ce cher Bourbaki.
Un peu comme Euclide pour la géométrie : il n'a inventé ni les cercles ni les polyèdres réguliers, et il est d'ailleurs probable qu'il n'ait pas rédigé seul ses Éléments.

Cordialement.