Tableau en 2D : nombre de chemins possibles

[ablablaha]

Bonjour,

Je m'empêtre depuis plusieurs jours sur un problème mathématique :

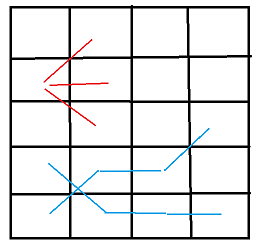
On a un tableau de 4 cases horizontales sur 5 verticales. Combien de chemins possibles y a-t-il pour passer de la gauche du tableau à sa droite, sachant qu'à chaque déplacement, on doit forcément passer à la colonne suivante (soit tout droit, soit en diagonale). Je vous ai fait un petit schéma. En rouge, les 3 directions possibles a partir d'une case. En bleu, deux possibilités de chemin pour aller de gauche à droite


Bon pour etre honnete, je connais la réponse, il y a 95 chemins possibles.
Ce que je cherche depuis plusieurs jours, c'est la formule qui permet de trouver ce nombre en fonction des dimensions du tableau.
Je veux pouvoir connaitre le nombre de chemins pour 50 cases horizontales et 6465465 verticales, je cherche LA formule, mais impossible pour mon niveau.

Si quelqu'un a le niveau, ca me serait très utile.

PS : j'ai vu que ca se rapproche du triangle de Pascal. C'est un peu plus compliqué cependant.
-----

[toothpick-charlie]

pour le tableau avec plus de 6 millions de lignes, je pense que si ce que tu cherches est une valeur approchée (de toutes façons ça va être un nombre énorme) tu peux négliger la question des bords, et alors la solution est très simple, puisqu'à chaque pas tu as 3 possibilités, donc pour un chemin partant d'une case donnée, et ayant n pas à faire, il y a 3^n chemins (3^49 dans le cas de 50 cases). Tous ces chemins sont évidemment distincts. Ensuite tu multiplies par le nombre de lignes du tableau... Pour le petit tableau en revanche il faut tenir compte de ce qui se passe sur les bords, et je ne vois pas d'astuce qui dispenserait de faire un calcul pénible.

[Tryss]

En dehors des cases "de bord" (les 49 premières et 49 dernières cases), pour chaque case de départ il y a 3^49 chemins possibles (3 choix a chaque passage de colonne)

Pour les 49*2 cases "du bord", c'est un peu plus compliqué a compter, mais on peut remarquer une certaine récurrence: Pour une case éloignée de n du bord sur la première colonne, alors il y a : le nombre de chemin d'une case éloignée de n-1 du bord pour le cas à 49 colonnes + le nombre de chemin d'une case éloignée de n du bord pour le cas à 49 colonnes + le nombre de chemin d'une case éloignée de n+1 du bord pour le cas à 49 colonnes.

A partir de là, tu peux facilement écrire un petit programme qui calcule (en remplissant un tableau), la valeur du nombre de chemins.

[Médiat]

Bonjour,

Quelques remarques :

1) Si on prend un tableau de n lignes et m colonnes, En posant N(i, j) le nombres de chemins pour atteindre la cellule (i, j), on a les relations : N(0, j) = N(n + 1, j = 0 et N(i, 1) = 1 (pour i entre 1 et n), N(i, j+1) = N(i-1, j) + N(i, j) + N(i+1, j), ce qui est facile à programmer avec un tableur

2) il y a une relation simple entre la somme d'un ligne et les valeurs de la première colonne (et de la dernière)

3) Cela a un rapport avec l'écriture en base 5 (2 digits successifs ne différant qu'au plus de 1)

4) vous pouvez regarder là : http://arxiv.org/pdf/0809.0551v1.pdf

[A voir en vidéo sur Futura]

[ablablaha]

Merci a vous, quelques précisions.

Deja quand je dis 50 cases sur 6millions, c'était un exemple, je reprécise que c'est la formule générale qui m'intéresse, pour x lignes et y colonnes.
Et je ne cherche pas un programme pour calculer, mais une formule. J'ai déjà réalisé sur excel des tableaux très simples qui me donnent toutes les réponses que je veux, mais je cherche une formule directe, qui ne m'oblige pas, pour trouver par exemple le résultat à la colonne 50, à trouver d'abord la 49 et donc la 48, et donc la 47,....

[Tryss]

Dans ce cas le papier qu'a link Médiat te donne une jolie formule :

Pour k lignes et n colonnes, le nombre de chemins est donné par




Ceci dit, pas sur que ce soit très pratique en pratique, il faudrait faire très attention aux erreurs d'arrondis pour des n et des k très grands

[ablablaha]

Je ne crois pas que cete dernière formule soit celle que je cherche
Je ne suis pas sur, car j'ai un bas niveau en maths. Du coup je me suis un peu familiarisé avec le sigma, mais en appliquant la formule avec 5 lignes et 4 colonnes, j'obtiens un résultat proche de 480 alors que je suis sur que la bonne réponse est 95.

Quelqu'un pourrait tester la formule rapidement avec 5lignes et 4 colonnes et me dire ce qu'il trouve ?

[Médiat]

Bonsoir,

C'est bien 95 :

0     1     1     1     1     1 0      5
0     2     3     3     3     2 0     13
0     5     8     9     8     5 0     35
0    13    22    25    22    13 0     95
0    35    60    69    60    35 0    259
0    95   164   189   164    95 0    707
0   259   448   517   448   259 0   1931
0   707  1224  1413  1224   707 0   5275
0  1931  3344  3861  3344  1931 0  14411
0  5275  9136 10549  9136  5275 0  39371
0 14411 24960 28821 24960 14411 0 107563
0 39371 68192 78741 68192 39371 0 293867

[ablablaha]

Mais je le sais que c'est 95, je le sais depuis le début, mais c'est une formule que je veux moi, pas un tableau et pas un programme, je veux une formule.
Tryss m'en a donné une mais je crois qu'elle n'est pas bonne. Et je demandait a ce que quelqu'un la vérifie justement avec l'exemple du tableau 4 sur 5, pour voir s'il obtient bien 95

[Tryss]

Ah, zut, la formule que j'ai donnée c'est pour les mots cylindriques (le bas communique avec le haut). La formule (plus complexe) pour le cas que tu souhaites est le théorème 2.4 du papier :



Et elle donne bien 95 pour n=4 et k=5

[ablablaha]

Je viens d'essayer de poser le calcul entier pour un tableau 3x3. La résultat est 17, mais moi j'obtiens 18,22 a peu près
Peux-tu vérifier ce dernier exemple pour etre sur que c'est la bonne formule stp ?

[Tryss]

J'ai effectivement fait une petite erreur de copie. La bonne formule :



Ce qui donne, pour k=3 :

Seuls les termes en j=1 et j=3 sont non nuls.

Pour

Pour

D'où

[ablablaha]

Ok, bon bah merci beaucoup pour ton aide, a la prochaine