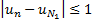suite de Cauchy bornée

[mondrook]

Bonjour, j'ai un problème avec la démonstration montrant qu'une suite de Cauchy est bornée. En se basant sur la définition suivante:
image001.png

Je ne comprends pas pourquoi on peut fixer epsilon valant 1 vu que la propriété doit être vraie pour toute suite de Cauchy?

De plus je ne comprends pas pourquoi l'inégalité suivante montre que la suite est bornée:
image003.png



Merci.
-----

[gg0]

Bonjour.

En attendant de pouvoir lire tes documents ("en attente de validation"), quelques idées.
* "la propriété doit être vraie pour toute suite de Cauchy" Oui, donc on le prouve pour une quelconque, la démonstration est valide pour toutes.
* l'idée de la preuve est qu'une suite finie est bornée (par son maximum et son minimum), et que si les termes d'une suite U sont tous à moins de 1 d'un terme U_k, ils sont tous entre U_k-1 et U_k+1. (si mon intuition de ta preuve est correcte).

Cordialement.

[Médiat]

Bonjour,

Vous devez démontrer que "Suite de Cauchy" ==> "Suite bornée", donc vous avez le droit d'utiliser toutes les propriétés de "Suite Cauchy" et en particulier si, telle propriété est vraie pour toute valeur de epsilon, elle est, en particulier, vraie pour epsilon=1.


Pour le deuxième point, j'aurais plutôt écrit : , et là les choses devraient être claires.

[gg0]

Ok, je vois tes formules.

Tu peux rédiger ta propre démonstration en utilisant des majorants et minorants de la suite finie des termes d'indices compris entre 0 et N1, puis ceux de la suite infinie des termes d'indices supérieurs à N1. Rédiger une preuve est le meilleur moyen de la comprendre.

Cordialement.

[A voir en vidéo sur Futura]

[mondrook]

Merci pour vos réponses. Je n'ai cependant pas tout saisi (je ne sais pas pourquoi je bloque là dessus)

Médiat: j'ai un soucis quand vous dites que si c'est vrai pour tout epsilon alors c'est vrai pour epsilon valant je comprends mais là dans les preuves que j'ai vu on considérait que si c'est vrai pour 1, alors ça l'est pour tout epsilon (c'est cela qui me pose problème).

gg0: Je suis d'accord sur le fait que refaire sois même la démonstration est le meilleur moyen de la comprendre. Ici j'ai l'impression de bloquer sur quelque chose de simple et je n'ai pas compris vôtre indication.

[Médiat]

Médiat: j'ai un soucis quand vous dites que si c'est vrai pour tout epsilon alors c'est vrai pour epsilon valant je comprends mais là dans les preuves que j'ai vu on considérait que si c'est vrai pour 1, alors ça l'est pour tout epsilon (c'est cela qui me pose problème).

Qu'est-ce que vous avez à démontrer qui utilise cela ?

Dans le cas présent, pour démontrer qu'une suite est bornée, il n'y a pas de epsilon (avec l'usage habituel) puisque ce qui doit être démontré, c'est



Qui est une formule existentielle, donc trouver un qui marche est suffisant.

[mondrook]

Vous avez raison Médiat, je n'avais pas fait attention. Ca paraît tellement évident.
Par contre avant de conclure il me reste le second point de ma question à éclaircir, c'est à dire comment à partir de:



je conclus que la suite est bornée car il y a la soustraction qui m'embête.

[Médiat]

étant une constante, il doit être assez facile de démontrer que . Le "1" à la fin de cette formule vient du choix de epsilon, si on avait choisi epsilon = 10, cela aurait modifier N_{10}, et il aurait fallu démontrer : , dans les 2 cas la conclusion est facile.

[mondrook]

Merci beaucoup Médiat, tout paraît évident maintenant.