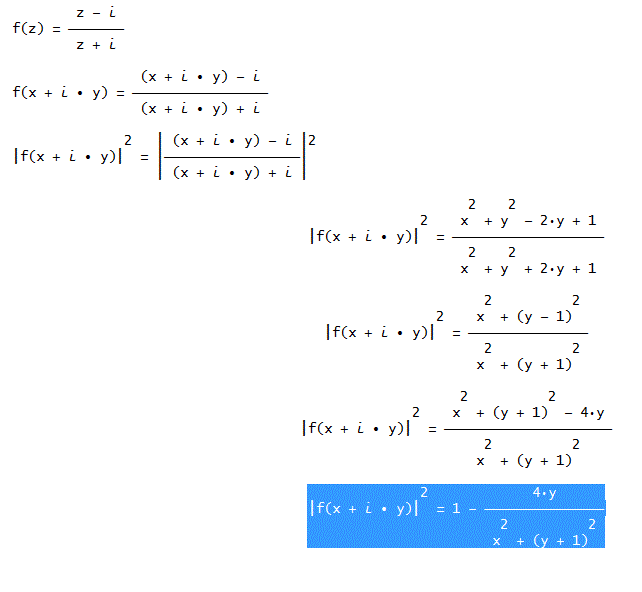Répresenter graphiquement un sous-ensemble d'un ensemble C !

[Lolaa06]

Bonsoir à tous ,

J'ai du mal à répresenter graphiquement un sous-ensemble d'un ensemble C donc j'espère que vous allez pouvoir m'aider.

Donc, l'enoncé est: On considère l'ensemble E=C\{i} et f: E --->C définie par f(z)=(z+i)/(z-1). Pour un nombre z e C, on note Re(z) la partie réelle de z et Im(z) la partie imaginaire de z.

Répresenter graphiquement le sous-ensemble de l'ensemble C défini par : F = { z e C, Im(z)>0 }

Que pouvez vous dire de l'image par f de cet ensemble F, noté f(F) ?

Que pouvez vous dire de l'image de l'ensemble f(G) ou : G = { z e C, Im(z)<0 }


Je ne sais vraiment pas par ou commencer.

En esperant d'avoir votre reponses,

Cordialement
-----

[minushabens]

Mais l'ensemble des complexes de partie imaginaire positive, tu vois ce que c'est quand-même?

[Lolaa06]

minushabens: malheuresement non là je ne vois pas !

[minushabens]

Tu n'as jamais entendu parler du "plan complexe"? : la représentaion de C comme un plan.

[A voir en vidéo sur Futura]

[polf]

Il y a une erreur sur l'espace de définition ou le dénominateur.

[Lolaa06]

Tu n'as jamais entendu parler du "plan complexe"? : la représentaion de C comme un plan.

Je m'excuse j'etais trop fatiguée cette nuit là je ne me souvienais de rien :A . Si bien sur que si , je connais le plan complexe mais cet exo je ne sais pas comment y repondre vu que si Im(z) > 0 répresente toute la partie positive d'axe d'ordonées (0 exclus) tandis que Im(z)<0 est le contraire, la partie négative d'axe d'ordonées ( 0 toujours exclus) .

Donc voilà comment le répresenter sur ma copie?

[Lolaa06]

Il y a une erreur sur l'espace de définition ou le dénominateur.

c'est-à-dire ??

[polf]

La fonction f(z) = (z+i) / (z-1) est définie sur E=C\{1} et non E=C\{i}

La résolution :
Partez de z=x+i.y et écrivez :

a+i.b = f(x+ i.y) = (x+ i.y+i) / (x+ i.y-1)
isolez y dans cette équation -> y = fct(a,b,x)

F est défini par y>0 et x qlq
déterminez b=fct2(a,x) / fct2(a,x) soit réelle
déterminer la relation entre a et b / fct(a,b=fct2(a,x),x)>0

de même pour G

[polf]

déterminez b=fct2(a,x) / fct2(a,x) soit réelle

Je voulais dire :
déterminez b=fct2(a,x) / fct(a,b,x) soit réelle

[Lolaa06]

Je voulais dire :
déterminez b=fct2(a,x) / fct(a,b,x) soit réelle

Au fait Polf, je viens de trouver la partie réelle et celle imaginaire de Z c-a-d:

y=(x+i)/(x-i)

y(x-i)=(x+i)

yx-iy=x+i

iy+i=yx-x

i(y+1)=x(y-1)

d'ou: Re(z)=x(y-1) et Im(z)=i(y+1)

Pour F={ z e C, Im(z) > 0 } on a i(y+1) > 0
y+1 > 0
y > -1

et pour G={ z e C, Im(z) < 0 } : i(y+1) < 0
y+1 < 0
y < -1

Apres je sais pas trop quoi faire.. :/

[polf]

Si z=x+iy
F est défini par x qlq et y>0
G est défini par x qlq et y<0

La frontière entre F et G est définie par x qlq et y = 0 : (S)
f(z)=(z+i)/(z-i)
pour y = Im (z) = 0
f(x) =( x+i)/(x-i)
f(x) = (x+i)^2/((x-i).(x+i))
f(x) = (x^2+2ix-1)/(x^2+1)
ABS(f(x))^2 = ((x^2-1)^2+4.x^2)/(x^2+1)^2
ABS(f(x))^2 = (x^4+1+2.x^2)/(x^2+1)^2
ABS(f(x))^2 = 1
lorsque x décrit R, (S), décrit le cercle de centre 0 et de rayon 1

Si maintenant x qlq et y >0
f(z)=(z+i)/(z-i)



F est l'intérieur strict du cercle de centre 0 et de rayon 1

G est l'extérieur strict du cercle de centre 0 et de rayon 1

La démonstration n'est pas complète (il faudrait démontrer que TOUT l'intérieur du cercle est compris dans F et que TOUT l'extérieur du cerlce est compris dans G)