Calcul de volume/intégrales triples
Bonjour à tous,
Je viens chercher votre aide car j'ai deux exercices de maths qui me posent problème...
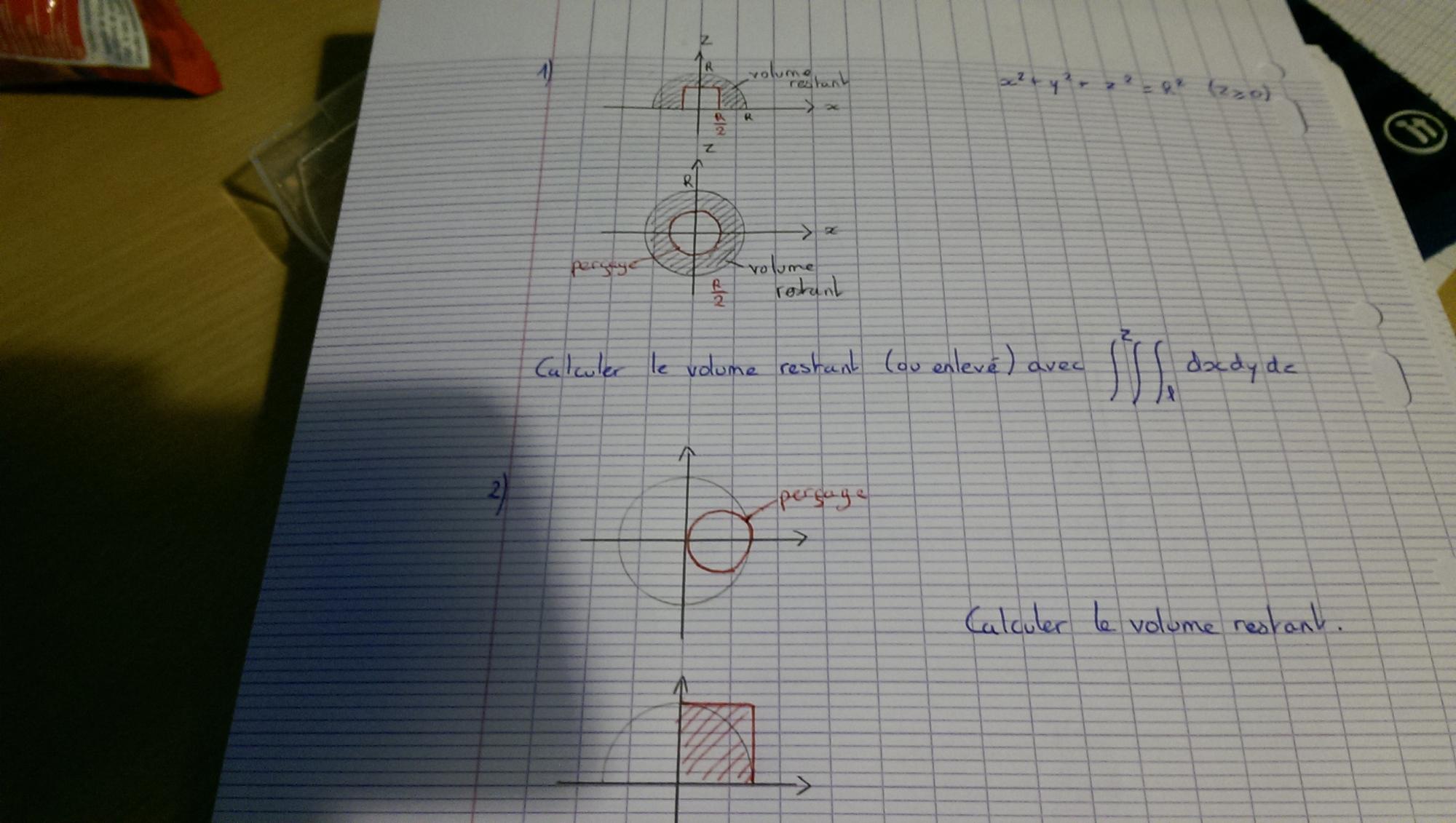
Je dois calculer le volume restant après un perçage à l'aide d'une intégrale triple...le problème c'est que je n'y arrive, je ne sais pas du tout comment faire...pouvez vous m'aider s'il vous plait?
Voici l'énoncé :
Merci à tous?
Réponse ici : http://forums.futura-sciences.com/ma...ces-forum.html
Merci mais ça ne m'aide pas vraiment...
Bonjour,
Si vous commenciez par nous informer sur votre travail, cela permettrait de savoir comment vous aider (vous donner la réponse étant la pire façon de ne pas vous aider), et cela motiverait des contributeurs à passer du temps pour vous !
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
C'est quand même dommage de devoir expliquer ce qu'il y a dans un lien ....
Cordialement.
Bonjour,
Et bien ce que j'ai donné sur la photo est tout ce que j'ai...nous avons seulement le schéma et nous devons trouver le volume restant...le problème c'est que nous n'avons jamais fait ça. Nous avons seulement utilisé les intégrales doubles pour calculer l'aire.
Donc ne sachant pas utiliser les intégrales triples, je ne vois même pas par où commencer...
Il n'y a aucune différence fondamentale entre intégrale double et triple, pour quelques exercices corrigé, voir par exemple : http://iecl.univ-lorraine.fr/~Gerard...ARTICLE/EN.pdf
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
Ok.
Si tu ne sais rien sur les intégrales triples, tu ne peux pas faire ton exercice. C'est terminé !
Si tu sais comment les calculer, il te suffit de savoir que le volume d'un solide est l'intégrale triple sur le solide de 1. Il est souvent préférable de décomposer le solide en plusieurs parties.
Pour le premier exercice, la question est idiote, car à condition de connaître la hauteur du cylindre enlevé, c'est un exercice pour bons élèves de troisième. Et on peut mener le calcul avec les intégrales triples pour reproduire le calcul du collégien.
Le deuxième demande un peu plus de travail.
A noter : On peut aussi calculer ces volumes avec des intégrales doubles.
Cordialement.
NB : On ne commencera pas les calculs avant toi.
D'accord, merci pour vos réponses et merci pour le lien!
Donc si j'ai bien compris il vaut mieux commencer par décomposer le solide en plusieurs volume...
Si j'appelle V1 le volume de la demi-sphère, V2 le volume juste au-dessus du rectangle rouge (je me suis trompée sur le dessin, les cotes touchent le haut de la demi-sphère). Et enfin V3 le volume du rectangle rouge.
Pour avoir le volume total on fait V1-V2-V3...est-ce déjà un bon début?
Bonjour:
D'apres ce que j'ai compris vous voulez calculez le volume restant du perçage d'une sphère avec pour le premier cas un Cuboïde rectangulair, pour le second cas un cylindre de base circulaire a pour centre le meme que la sphere , le troisieme par un cylindre dont le centre de ça base appartient au rayon de la sphere , le quatrième cas percer par un Cuboïde celon le schéma.
Dans les 4 cas suivant le schéma l'important dans ce calcule en utilisant les intégrales triples est de bien délimité le domaine de ce volume le reste c'est du calcule .
Cordialement
Bonjour :
Aussi d'apres votre schéma partie 2) ça correspond parfaitement à la Fenêtre de Viviani.
Amicalement
Tout dépend de l'énoncé. Celui qui est dessiné au premier message donne seulement V1-V3. Mais c'est toi qui as l'énoncé.Pour avoir le volume total on fait V1-V2-V3...est-ce déjà un bon début?
Merci pour vos réponses!
Viviani? Et comment l'utiliser avec les intégrales??
Sinon pour le 1 voila ce que j'ai fait...mais je ne suis pas sure pour le V1-V2-V3...pour le 2), je ne sais pas du tout comment faire
Je suis d'accord pour V1 (volume d'une demi-sphère). Pour la suite, j'ai l'impression que tu n'as pas utilisé la dimension du perçage. Elle permet de déterminer h, qui n'est pas une donnée du problème initial. La formule que tu as trouvée est bien celle d'une calotte sphérique. par contre, je ne comprends pas le calcul de V3, de volume Pi.r²(R-h) où r est le rayon du cylindre, donc est plus petit que R.
Donc j'ai l'impression que tu as oublié les données de ton problème.
Cordialement.
Merci de ta réponse!
Donc pour V2 tu penses que c'est bon?
Pour V3, si j'ai bien compris, c'est bon mais je n'ai pas pris les bonnes données c'est ça?
Non,
je t'ai dit que pour V2 la formule est bonne, mais pas celle attendue (il n'y a pas de h sur ton énoncé); et pour V3, c'est carrément faux. Ne lis pas à partir de tes envies, essaie de comprendre ce qui est écrit.
Désolée, mais ça fait des heures que je suis sur ces exercices, je commence à en avoir un peu marre lol
V3, c'est la formule qui est fausse? Ou les bornes peut-être?
Pour V2, même si c'est moi qui incorpore la valeur h ça ne marche pas? Quelle serait la formule approprié?
Merci pour ton aide
Bon sang,
regarde ton énoncé. J'ai du mal à lire, mais il semble qu'il y a une cote pour le perçage. pas pour la hauteur le la calotte qui "saute".
C'est ton énoncé, c'est à toi de le connaître. Fatigue ou pas. Si tu réfléchis à côté de l'énoncé, tu te fatigues pour rien !
Alors au lieu d'utiliser h qui n'existe pas, j'aurais dû prendre R/2?
Si c'est R/2 qui est marqué sur ton premier schéma, c'est bien la donnée de l'exercice, et tu dois tenir compte de cette donnée pour le faire. Donc l'utiliser pour le volume du cylindre (V3) et pour calculer h.
Cordialement.
NB : Les deux perçages sont faits à la même dimension !
Dernière modification par gg0 ; 19/12/2014 à 10h04.
Merci pour ton aide, je pense avoir réussi en trouvant (racine de 3*Pi*R^3)/4 pour le volume restant...
Par contre pour l'exo 2 je ne vois pas comment faire...vu qu'effectivement les deux perçages sont de même dimensions, je pense que c'est a peu près pareil non?
L'exercice 2 est un peu différent, car on a un volume d'un seul tenant à calculer. Tu aurais d'ailleurs pu faire ça pour le premier. l'idée est de se ramener à une intégrale double. Je suppose que la demi sphère est posée sur le plan xOy. Une fois percée verticalement, l'intégrale triple du volume s'écrit facilement comme intégrale double sur x et y de l'intégrale de 1 sur z, z variant de 0 à une valeur maximale f(x,y). Ce qui nous ramène à intégrer f(x,y) sur la surface, y=f(x,y) étant l'équation de la surface supérieure de la sphère percée.
Dans les deux cas, il y a intérêt à exploiter les symétries (2 axiales pour le 1, une axiale pour le 2).
Bons calculs !
Aaaaah d'accord, je vois! Je vais essayer ça alors, merci pour ton aide
Bonjour:
Pour ce qui est de la deusiemme partie , je veux dire la demi-sphere percer par un cylindre (pour le calcul du volume restant ) :
@gg0: Attention si on vois bien sur la photos la demi-sphere est poser sur le planest non sur le plan
à moin que Squirrel02 a changer de position pour la sphere.Envoyé par gg0
Cordialement
Je n'ai pas trop fait attention aux notations, j'ai du mal à lire la photo de départ (prise de travers !) et avec les deux schémas, j'y vois deux axes Oz !! Donc j'ai précisé ma dénomination des axes de repère (leur nom n'a pas d'importance en soi).
mais tu as peut-être meilleure vue que moi
Bonjour:
@Squirrel02:Toute est faux , simple raison vous calculer
Ccordialement
