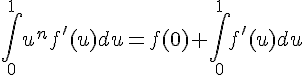Intégrale

[invite5499ba97]

Bonjour à tous, j'aimerai avoir un peu d'aide pour faire cet exercice:
Soit f de classe C¹ de [0,1] dans R et bijectif de [0,1] dans lui même tels que et ^-1 sont C¹ et
Montrer f(1) = 0
Montrer f est la fonction nulle.

J'ai commencé par faire un changement de variable afin de calculer l'intégrale mais je ne vois pas comment je pourrai tomber sur 0 à partir de là.
Merci d'avance
-----

[invite93e0873f]

Bonjour,

J'imagine que vous avez fait le changement de variable (justifié en raison des hypothèses sur ), de sorte que votre égalité devient .

Or, en vertu du théorème fondamental du calcul, , donc .

De ceci, nous pouvons voir qu'il manque une hypothèse à votre problème. En effet, si est une constante non nulle, alors cette dernière équation devient , bref , d'où .

Je présume que votre égalité doit tenir quel que soit n.

[invite93e0873f]

Je présume que votre égalité doit tenir quel que soit n.

... dans quel cas c'est assez facile, puisque la suite est uniformément bornée par les fonctions 0 et 1 et puisqu'elle converge (uniformément sur les intervalles de la forme ) vers la fonction nulle.

[invite5499ba97]

Oui, c'est tout à fait ça, j'ai presque obtenue cette nouvelle égalité, il y a juste une différence au niveau des bornes d'intégrations.
Je suis désolé mais je ne comprends toujours pas comment obtenir l'égalité avec 0 a partir de la nouvelle égalité. Faut-il résoudre pour trouver f(0)?

Sinon vous avez bien raison, l'égalité est bien quelque soit n mais je n'ai pas oublié de préciser d'autres hypothèse, il en manque réellement une.

[A voir en vidéo sur Futura]

[invite93e0873f]

Je suis désolé mais je ne comprends toujours pas comment obtenir l'égalité avec 0 a partir de la nouvelle égalité. Faut-il résoudre pour trouver f(0)?

Je ne suis pas certain de comprendre votre question, mais si vous parlez de l'équation que j'ai écrite, elle ne vous permet certainement pas de conclure que f(1) = 0... je donnais un contre-exemple sous l'hypothèse (implicite) selon laquelle un seul n suffisait.

[invite5499ba97]

Non, je ne parlais pas de celle là mais plutôt de
Permet elle de conclure?

[invite93e0873f]

Procédons par étape.

La première étape est de montrer que f(1) = 0. Cela se déduit des équations quel que soit . L'idée maîtresse ici est illustrée au message #3.

Si l'égalité tient aussi pour , alors il suffit de comparer l'équation au théorème fondamental du calcul pour en déduire que .

-----

La deuxième étape est de montrer que f(u) = 0 pour tout u. C'est plus ardu, puisque les conditions intégrales ne sont de prime abord que des conditions globales. Il faut que j'y pense encore...

[invite5499ba97]

D'accord, je vais maintenant essayer de faire tout ça avec toutes les indications que vous m'avez donné. Merci beaucoup pour votre aide Universus

[invite93e0873f]

Bon, je vois mal comment résoudre « simplement » la seconde partie. Cependant, j'ai un argument très suggestif.

Puisque pour tout , il en résulte que pour tout polynôme P, voire pour toute fonction analytique P définie sur [0,1]. En vertu du théorème de Stone-Weierstrass, nous pouvons approximer autant que nous le souhaitons n'importe quelle fonction continue, donc en particulier : , il existe un polynôme P tel que pour tout u. Ainsi,

, d'où



En prenant , il en résulte que , donc (par continuité de f') pour tout u.