Bonjour
Je lance deux point dans un plan, la probabilité d’appartenir à une droite est 1
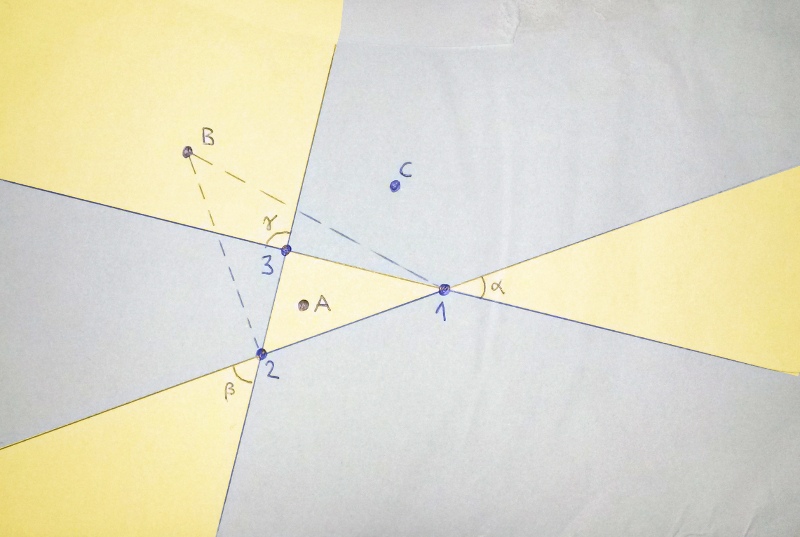
Je lance trois points, la probabilité est impossible à déterminer.
Un autre exemple :
Je lance 4 points, quelle-est la probabilité que les 4 point forment un triangle avec un point à l’intérieure du triangle ?
-----