Bonjour tous,
je dois intégrer une fonction "f(x,y)" sur un différents domaines triangulaires (cf. PJ) mais je me pose pas mal de questions et j'espère que vous pourrez y répondre.
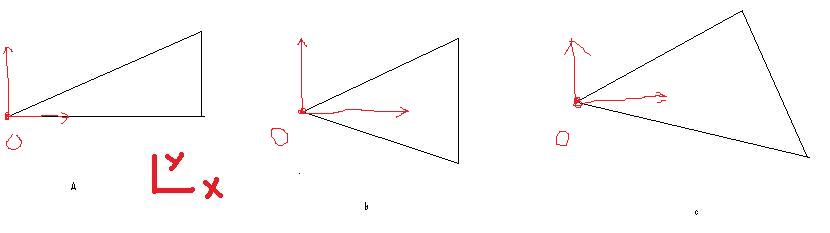
Si j'ai un triangle rectangle (cas A en PJ) :
je vois comment faire : je dois intégrer de Xmin à Xmax et de Y=0 à Y=equation hypothenuse
Si j'ai le double d'un triangle rectangle (cas B en PJ) :
- comme il y a symétrie je pense que le résultat sera deux fois le résultat du cas précédent mais es ce toujours vrai ?
- d'ailleurs je suis en train de me demander si le résultat ne devrait pas plutôt être 0 puisque j'ai exactement en même chose en dessous et au dessus de Y=0 ??
pour un triangle rextangle je vois commen faire mais pas dans le cas quelconque (cas C en PJ)
- maintenant je ne peux plus le balader suivant X et faire varier Y en respectant la droite qui va vers le haut car sinon je n'intégreger qu'une partie du triangle...
- comment doit on procéder pour ce type de forme ? on doit découcer en plusieurs sous espaces ?
je sais que ça fait pas mal de questions mais je suis pas mal perdu,
j'espère que vous pourrez m'aider
merci d'avance
bon WK
-----




 et
et