Casse-Tête Diabolique !
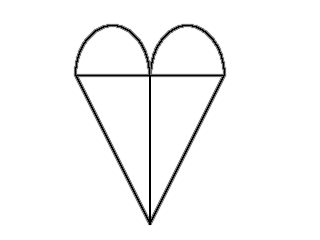
Bonsoir !
Aidez-moi ! J'en peux plus !
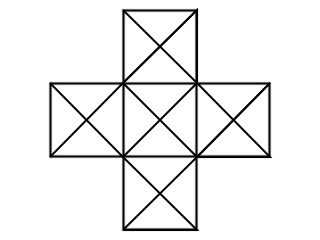
Le but du jeu est de trouver une manière d'effectuer ce tracé en levant le crayon au maximum 5 fois : j'ai trouvé 36000 manières de le faire en 6 fois, mais en 5 fois... c'est le vide total !
( Voici l' image en format JPEG pour les navigateurs qui ne supportent pas les PNGs)
HS : remarquez l'effet d'optique dans les coins de la figure que j'ai dessiné, amusant, non ?
Si tu sais dessiner une "maison" sans lever le crayon, ça marche en 5 fois sans trop de problèmes.
Oui, pour la maison, pas de problème...
Mais ce que j'ai omis de préciser ( oups ! ) ce qui l'est interdit de repasser par dessus un même trait...
moi je dis en quatre fois sans lever le crayon, qui dit mieux?
croisement de post loot
la donne est differente maintenant
quand a moi je vais aller dodoter...
En 5 fois... tu veux dire en levant le crayon 5 fois (donc en 6 tracés) ou en 5 tracés ?Envoyé par matthias
Il y a 12 sommets d'ou partent un nombre impair de segments. L'ors d'un tracé on trace un nombre pair de segments à tous les sommets ou on passe, sauf au point de départ et d'arrivée. Pour tracer un nombre impair de segments partant de 12 sommets différents, il faut nécessairement 12 points de départ ou d'arrivée, soit 6 tracés. Donc 5 levers de crayon.
En d'autres termes : Je demande à voir
5 levers de crayon, 6 tracés.
C'est aussi comme ça que je l'ai vu, mais en fait on aurait aussi pu interpréter ce graphe comme ayant 17 sommets.
Oui, 17 en tout. Je parle bien des sommets d'ou partent un nombre impair de segments.
Oups, oui désolé, c'est vrai que la démonstration marche que l'on considère 12 ou 17 sommets, il y en a toujours 12 d'ordre impair.
Bonjour, par 5 fois, j'entendais 5 tracés !
Hum... sinon, j'ai pas tout compris ce que vous avez écrit, mais en gros, vous avez démontré qu'on ne peut pas le faire en moins de 6 tracés, c'est ça ? ( ou alors, j'ai vraiment rien compris ?)
Oui, c'est ça. Il est impossible de le faire en moins de 6 tracés, donc en levant le crayon moins de 5 fois. C'est bien le but du jeu, non ? Donc tu as gagné.Bonjour, par 5 fois, j'entendais 5 tracés !
Hum... sinon, j'ai pas tout compris ce que vous avez écrit, mais en gros, vous avez démontré qu'on ne peut pas le faire en moins de 6 tracés, c'est ça ? ( ou alors, j'ai vraiment rien compris ?
OK ! Merci beaucoup !
Tenez, tant que vous êtes lancés, j'en ai un deuxième sur lequel je m'excite comme un forcené sans en trouver la réponse, le voici :
( JPEG )
Pareil, ici le but est de réaliser cette figure en 1 seul tracé cette fois, sans lever le crayon évidemment.
En deux tracés. Impossible de faire mieux.
Compte les sommets d'ordre impair (ceux d'ou partent un nombre impair de lignes). S'il y en a deux ou aucun, c'est possible. S'il y en a 4 ou plus, c'est impossible.
Moui...
En fait, en relisant tout tes posts, j'en déduis, qu'en règle générale, on peut déterminer le nombre de tracés minimaux en comptant le nombre de sommets d'où partent un nombre impairs de lignes, on divise ce nombre par deux puis on arrondit à l'entier supérieur : le résultat obtenu correspond au nombre de tracés minimaux pour représenter la figure : correct ?
Oui, sauf qu'il n'y a pas besoin d'arrondir : le nombre de sommets d'ordre impair est nécessairement pair.
OK, je sens que cette propriété va beacoup me servir
Encore merci !
