Treilli des sous-groupes

[Perfectina]

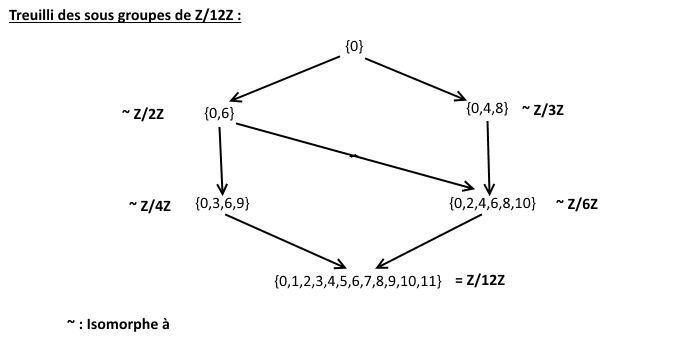
Bonsoir

Auriez-vous une définition simple (claire) du treilli de sous-groupes ? J'ai beau chercher un peu partout, soit je n'en trouve pas, soit je ne les comprends absolument pas (sur wikipédia par exemple)...

Par exemple, on me demande de calculer le treilli des sous-groupes de (Z/pZ, +), p nombre premier...
Ou encore le treilli des sous-groupes de (Z/4Z, +) ou de (Z/2Z * Z/2Z, +)...

Je révise un examen (je n'ai pas les cours) et j'aimerais être au point ! Je suis en L2 de maths.

Je vous remercie d'avance !
-----

[Seirios]

Bonsoir,

Il me semble qu'il suffit de décrire tous les sous-groupes du groupe en question, et de préciser quand l'un est inclus dans l'autre.

[Perfectina]

Ok merci

Et je vais me permettre une autre question : qu'est-ce que les sous-groupes de (Z/nZ, +) ? Je sais que pour (Z, +) ce sont les nZ, mais pour (Z/nZ) je n'arrive pas à voir...

D'avance merci ^^

[Amanuensis]

Exemple pour Z/4Z = {0, 1, 2, 3}, les sous-groupes sont {0}, {0, 2} et {0,1,2,3}

[A voir en vidéo sur Futura]

[Tryss2]

Et plus exactement, les sous groupes de Z/nZ sont engendrés par un élément d, où d divise n.

Par exemple, pour Z/12Z, le treillis des sous groupes ressemble à ça :

Erreur dans l'image ^^

[Tryss2]

Il ne devrait pas y avoir d'erreur dans celui là :

[Amanuensis]

Hmm... On pouvait laisser trouver...

(On ne voit pas les images, mais pour Z/12Z, le treillis c'est 8 )

[Tryss2]

Nan, mais après je demande le treillis de S5

[Amanuensis]

[Réponse à l'aparté]

Je me suis coltiné un jour le groupe du cube à la main, avec lequel on peut s'aider visuellement pourtant. Pas triste, mais on y arrive...

[Perfectina]

Je vous remercie !
J'ai bien compris le schéma, on prend en fait en compte les diviseurs de 12 (de n).
Mais quand on a un produit, Z/3Z * Z/8Z (tout autre exemple est la bienvenue ), par exemple... on s'y prend comment ?

Je précise que ce ne sont absolument pas des devoirs, j'essaye simplement d'être au point sur cette leçon et de me préparer à l'examen... !