Bonjour,
Pour faire un petit fil rouge de vacances, voici quelques questions/interrogrations/reflexions un peu vagues, mais qui me trottent dans la tête depuis pas mal de temps ( ici par exemple) sur la discrimination des objets géométriques parmi les objes topologiques.
Etant surtout interessée par la géométrie differentielle, j'ai lorgné récément sur ce qu'il se fait chez les voisins d'à coté i.e les géométres complexes/algébristes, et je fut veritablement surprise de découvrir la richesse des structures additionnelles que possède naturellement la cohomologie de leurs objets (et frustrée également par le fait que je suis pas capable de comprendre les considérations qui permettent de les mettre en évidence).
Notament, il y a un phénomène tres interessant: la structure de Hodge sur la cohomologie rationelle d'une variété analytique complexe qui soit compacte, Khalerienne et lisse.
Je suis tres loin de comprendre les details de la théorie, mais de ce que j'en sais, la structure complexe, se traduit par la donnée d'un (champ) d'operateur differentiels (le fameux "d barre") qui se traduit par une filtration sur la cohomologie de la variété (tensorisée par C), qui depend de la structure complexe.
Ma question est vague et generale, peut on transposer de telles constructions au cas des variétés differentiables réelles? Des variétés Riemanniennes?
Ce dernier cas me parait favorable, car on possède la aussi un opérateur differentiel privilégié, la connexion.
Peut on discriminer parmi les espaces topologiques ceux qui proviennent de variétés differentiables uniquement en regardant ses structures spéciales sur la cohomologie? (il y a deja des faits basiques, qui permettent de faire un premier tri grossier, par exemple le fait que les groupes de cohomologie doivent etre de type finis sur Z, et du moins dans le cas compact, présenter une dualité de Poincaré).
Peut on faire varier la structure Riemanienne au sein d'une meme classe de diffeo de variété diff (par la je veux dire, peut on la paramétrer convenablement, par une variété de dimension finie)?
Bon, je vais e pencher sur ces questions pendant mes vacances, et je dirait ici si je progresse ou pas dans ma conaissance de ces choses là, qui me paraissent véritbalement passionantes!! N'hesitez pas si vous avez des questions/réponses/commentaires/remarques.
Et Joyeuses Fetes.
-----




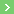
 , on obtient la cohomologie de Dolbeault, et de la même manière qu'on scinde la cohomologie de Dolbeault sous forme de sous espaces propres ( par une sorte de diagonalisation implicite de la structure complexe :
, on obtient la cohomologie de Dolbeault, et de la même manière qu'on scinde la cohomologie de Dolbeault sous forme de sous espaces propres ( par une sorte de diagonalisation implicite de la structure complexe :  .
.