Déterminer si une suite de nombres est aléatoire

[Juzo]

Bonjour à tous, je me demandais s'il était possible de déterminer la probabilité qu'une suite de nombre soit aléatoire (sûrement avec une marge d'erreur qui diminuerait avec le nombre de valeurs de la suite)

Je viens de regarder sur Wikipedia, apparemment la façon de définir une suite aléatoire a mobilisé des mathématiciens pendant longtemps au 20^ème siècle (lien ci-dessous)
https://fr.wikipedia.org/wiki/Suite_aléatoire

Il existerait 3 modes de définition qui semblent concourants, mais je n'ai pas trouvé de trace de ce calcul de probabilité....
Je vous propose d'imaginer ce que l'on pourrait faire si on maîtrisait un tel calcul.

Deux propositions :
- on pourrait par exemple étudier la suite des décimales de Pi, e ou encore racine de 2... Certains de ces nombres pourraient-ils avoir une suite aléatoire, et d'autres non? Une suite non aléatoire signifierait-il qu'il y a une "structure" sous-jacente au nombre ?
- on pourrait aussi vérifier en mécanique quantique si la particule choisit bien aléatoirement sont état lors de la réduction du paquet d'onde (on sait qu'il n'y a pas de variable cachée, mais est-on sûr que la valeur prise est bien aléatoire ?)

Bien sûr on ne pourrait calculer que des probabilités...

Avez-vous d'autres idées ? Sinon des propositions de calculs de probabilité que d'autres auraient plaisir à démonter seraient marrants aussi !

En fait, déterminer si une suite est aléatoire me paraît si intimement lié au des mystères fondamentaux, qu'il me semble impossible d'y parvenir un jour. Je sais, ce n'est qu'une impression, même pas une opinion !
-----

[gg0]

Bonsoir.

La suite des décimales de pi n'est pas aléatoire, puisqu'on peut toutes les déterminer (en théorie). Je ne vois pas ce que la mécanique quantique vient faire dans une question de maths.

Sinon, ce n'est pas 5 mn de réflexion personnelle qui feront avancer un problème sur lequel des mathématiciens de haut niveau et très inventifs ont passé des années à réfléchir. Avec les définitions actuelles de "suite aléatoire", la probabilité qu'une suite finie soit aléatoire est ... 0. En prenant des suites commençant par 0, une suite finie correspond à un décimal pris au hasard dans [0;1]; comme l'ensemble des décimaux est de mesure nulle, la proba est nulle.

Cordialement.

[Dlzlogic]

Bonsoir,
Le TCL précise que toute expérience de même loi produit une répartition normale.
Ca c'est une chose claire et nette.
Maintenant il faut préciser ce que signifie "aléatoire". Dans le cas de la suite des décimales de pi (exemple cité), la suite des caractères inscrits dans cette suite ont une répartition normale. Pour le comprendre, imaginons que les caractères utilisés pour les écrire ne soient pas du type "décimal", mais octal, hexadécimal, centennale etc.
Bien-sur, les caractères écrits ne sont pas aléatoires, puisqu'il correspondent à un réalité : l'écriture décimale du nombre pi.
Le caractère "aléatoire" signifie que la présence de chaque élément (sa valeur, son graphisme, sa représentation etc.) ne dépend que du hasard.
Il est très important de savoir que la répartition des résultats d'expérience aléatoire est conforme à la répartition normale (loi de Gauss et TCL).

Ce problème appliqué à la mécanique quantique est plus compliqué. En effet, la répartition n'est pas conforme à la répartition normale. Le Pr Jacques Harthong a expliqué cela en disant que le loi normale (Gauss, TCL) s'applique aux éléments "observables", ce qui n'est pas le cas lorsqu'il s'agit de l'EPR.
Pour se convaincre du caractère "aléatoire" de la présence des caractères décimaux du nombre pi, il suffit de prendre cette valeur (un millier de décimales par exemple), compter l'apparition de chaque chiffre, la différence à la moyenne théorique, calculer l'écart type et reporter les différents comptages : on obtient une courbe de Gauss.
Ensuite, on fait le même chose en prenant les caractères 2 par 2 (numération en base 100), on obtient encore une courbe de Gauss.
On peut faire le même type d'expérience avec un jeu de pile ou face, un dé à 20 faces etc, on obtient toujours la même courbe de Gauss.
Bonne simulation.

[invitec998f71d]

Je pense que la question posée est de savoir si pour de telles suites il y a un algorithme derriere. çà fait penser au test de turing. Converse t on avec une machine ou avec un etre humain.
A propos je viens de voir qu'un programme vient de battre 5 fois de suite au go le champion d'europe.

[A voir en vidéo sur Futura]

[invite9dc7b526]

Il existe des tests de qualité d'une suite de nombres pseudo-aléatoires. Le test dit des "runs up and down" par exemple.

[Amanuensis]

Le TCL précise que toute expérience de même loi produit une répartition normale.

Par exemple une expérience dont une sortie scalaire suit la loi est uniforme sur [0,1] aura une répartition normale, c'est à dire celle d'une loi gaussienne? Intéressant...

[Matmat]

Bonsoir,
Le TCL précise que toute expérience de même loi produit une répartition normale.
Ca c'est une chose claire et nette.
...
Il est très important de savoir que la répartition des résultats d'expérience aléatoire est conforme à la répartition normale (loi de Gauss et TCL).

Lancez 1 dé , chaque chiffre a 1 chance sur 6 de sortir , il n'y a pas de gaussienne .
Lancez 2 dés , c'est la SOMME des deux qui fait une gaussienne .

Pour se convaincre du caractère "aléatoire" de la présence des caractères décimaux du nombre pi, il suffit de prendre cette valeur (un millier de décimales par exemple), compter l'apparition de chaque chiffre, la différence à la moyenne théorique, calculer l'écart type et reporter les différents comptages : on obtient une courbe de Gauss.

Dans les décimales de pi , chaque chiffre apparaît 1 fois sur 10 .

[gg0]

Amanuensis, Matmat,

ça fait des années que ce triste sire raconte ses énormités, sur divers forums; certains l'ont exclu. Mais il détient la vérité révélée !!

Cordialement.

[gg0]

Matmat,

La loi de la somme des deux dés n'a rien d'une gaussienne, d'ailleurs c'est une loi discrète. mais même l'allure (en toit) est assez loin de celle de la loi de Gauss. Par contre, en lançant de plus en plus de dés, on obtient une répartition discrète qui s'approxime de mieux en mieux par une gaussienne.

Cordialement.

NB : la loi de Gauss est une loi limite dans ces situations, ce qui justifie de l'utiliser comme approximation dans certaines circonstances, et généralement, au voisinage de la moyenne.

[Juzo]

La suite des décimales de pi n'est pas aléatoire, puisqu'on peut toutes les déterminer (en théorie).

Très juste, mais comme le dit Dlzlogic, les décimales de Pi semblent suivre la loi de probabilité d'une variable aléatoire. Comment doit-on qualifier la répartition de ces décimales pour être plus juste ?

Pour se convaincre du caractère "aléatoire" de la présence des caractères décimaux du nombre pi, il suffit de prendre cette valeur (un millier de décimales par exemple), compter l'apparition de chaque chiffre, la différence à la moyenne théorique, calculer l'écart type et reporter les différents comptages : on obtient une courbe de Gauss.

J'aimerais faire la simulation mais je n'ai pas bien compris ce point. Comment doit-on reporter les différents comptages ? On réalise plusieurs expériences sur des intervalles de 1000 décimales et on reporte tous les résultats ? La courbe de Gauss serait centrée sur la moyenne théorique ?

Je comprends seulement qu'on pourrait calculer la moyenne et l'écart-type de n décimales de Pi, et vérifier que ces valeurs ce rapprochent de la moyenne et l'écart-type d'une loi uniforme : partie entière d'une loi uniforme sur [0 ; 10[.
Merci

Sinon, ce n'est pas 5 mn de réflexion personnelle qui feront avancer un problème sur lequel des mathématiciens de haut niveau et très inventifs ont passé des années à réfléchir.

Je m'en doute, c'est au plus un bon exercice pour se familiariser avec ce domaine, pour ceux qui comme moi le découvrent.

Avec les définitions actuelles de "suite aléatoire", la probabilité qu'une suite finie soit aléatoire est ... 0. En prenant des suites commençant par 0, une suite finie correspond à un décimal pris au hasard dans [0;1]; comme l'ensemble des décimaux est de mesure nulle, la proba est nulle.

Si la suite finie a n chiffres, il existe un nombre fini de nombres à n décimales dans [0 ; 1[ ...
Les deux définitions suivantes semblent utilisables pour une suite finie (extraits wikipedia)
-Une suite est aléatoire au sens de Martin-Löf si elle ne possède aucune propriété « exceptionnelle et effectivement vérifiable »
-« Sur la base de ces considérations, il peut apparaître naturel de définir une suite sans régularité, ou suite finie aléatoire, comme une suite qui pour être calculée demande en gros un programme aussi long qu'elle même10. »

La 3ème définition implique les martingales, à mon avis elle marche aussi, ces trois-là étant équivalentes

Alors peut-on calculer la probabilité qu'une suite finie soit aléatoire, ou est-ce indécidable ? Pour donner un exemple intuitif, il me paraît plus probable que la suite 5468761327 ait été obtenue en tirant 10 fois un dé à 10 faces, que la suite 9999999999... (Même si les deux tirages sont équiprobables)

Pour ce qui est de la MQ, je citerais une phrase qu'on prête à Einstein :"Dieu ne joue pas aux dés !". Moi ça me passionne de savoir si on peut déterminer s'il est possible que certains phénomènes physiques soient aléatoires...

Merci en tout cas pour vos éclairages !

Cordialement,

[invite51d17075]

Si la suite finie a n chiffres, il existe un nombre fini de nombres à n décimales dans [0 ; 1[ ...
Les deux définitions suivantes semblent utilisables pour une suite finie (extraits wikipedia)
-Une suite est aléatoire au sens de Martin-Löf si elle ne possède aucune propriété « exceptionnelle et effectivement vérifiable »
-« Sur la base de ces considérations, il peut apparaître naturel de définir une suite sans régularité, ou suite finie aléatoire, comme une suite qui pour être calculée demande en gros un programme aussi long qu'elle même10. »
...........
Alors peut-on calculer la probabilité qu'une suite finie soit aléatoire, ou est-ce indécidable ? Pour donner un exemple intuitif, il me paraît plus probable que la suite 5468761327 ait été obtenue en tirant 10 fois un dé à 10 faces, que la suite 9999999999... (Même si les deux tirages sont équiprobables)
,

bonjour,
il me semble qu'il est bien inutile de citer Einstein dans ce cadre.
( Et "pis" ça devient pénible, quand même)
Ensuite les deux suites finies que vous citer sont bien "équiprobables" , alors pourquoi penser l'inverse.

Enfin, les deux définitions que vous proposez ne sont pas équivalentes.
L'une semble évoquer un aspect aléatoire total, et l'autre partiel.
Par exemple : dans quel cadre mettez vous la suite sin(n) ? ( dont l'équiprobabilité n'est pas parfaite )

[gg0]

Juzo :

Pour l'instant, on ne sait pas grand chose des décimales de Pi. par exemple sont-elles équiréparties ? On ne sait pas. Pour les premiers milliards de décimales, les fréquences sont très proche, mais rien n'interdit que ça change après le 10^2000000 chiffre, le 1 apparaissant une fois sur 2. On ne sait pas non plus si Pi est une "nombre univers", c'est à dire si tout entier apparaît au moins une fois dans la suite des décimales (comme dans 0,1234567891011121314...)

Je n'ai pas trop compris non plus comment Ammanuensis fait apparaître sa courbe de Gauss avec une statistique sur 10 individus (Les 10 chiffres)

Enfin, la caractérisation de Martin-Löf pose d'évident problèmes, elle rappelle la définition du "plus petit entier non définissable en moins de onze mots" que l'on vient de définir en 10 mots. Ou le "plus petit entier sans particularité".
Dans tous ces cas, il ne s'agit pas de mathématiques.
la définition par les programmes est utilisable en théorie, pas en pratique. Conséquence : la plupart des suites finies sont "aléatoires", mais il est difficile d'en produire une qui le soit. Par exemple, la suite 1123581321345589144233377610 semble assez aléatoire mais se construit sur un principe très simple (je te laisse le voir)

Cordialement.

[Juzo]

Je citais cette phrase d'Einstein car elle aurait été formulée dans le cadre du paradoxe EPR en mécanique quantique, dont on parlait plus haut. Je ne disais pas que je partage son avis évidemment, mais restons aux maths.

Wikepedia (ce n'est pas wikipedieu, mais quand même), nous dit que ces définitions sont équivalentes. Ça me parait intuitif, car si un nombre n'a aucune propriété particulière, comment écrire un programme plus court que ce nombre pour le décrire ?

[Juzo]

Ps ansset : les suites 1 et 2 sont équiprobables, mais la 1 ayant moins de propriétés exceptionnelles que la 2, elle appartient à une "classe" plus grande de suites aléatoires, elle aurait donc plus de probabilité d'être une suite aléatoire

[Matmat]

Pour la suite 9999999999 , tu peux dire à un programme le premier terme et lui faire calculer tous les autres en fonction du terme précédent , idem avec la fibonacci de gg0 ( ici tu fais la fonction avec les deux termes précédent ) . d'aprés les définitions de wiki ce ne sont pas des suites aléatoires .

[Juzo]

Merci pour cette réponse que je viens de lire gg0. C'est justement quand un ami m'a parlé de la possibilité que pi qoit un nombre univers que j'ai pensé a ces questions.

Bien vu matmat, en fait la suite 9999999999 peut être définie par une expérience aléatoire mais n'est pas une suite aléatoire je confondais les deux.

[Dlzlogic]

Bonsoir,

Par exemple une expérience dont une sortie scalaire suit la loi est uniforme sur [0,1] aura une répartition normale, c'est à dire celle d'une loi gaussienne? Intéressant...

Ben oui, cela ne fait aucun doute. Naturellement, il s'agit de la répartition des écarts à la moyenne dont parle le TCL.

Une petite expérience facile à réaliser.
Avec un générateur de nombres aléatoires, on tire à pile ou face.
On groupe les résultats par 4 (ou 5) successifs.
En attribuant 0 ou 1 suivant la parité, on forme un nombre binaire de 16 (ou 32, suivant ce qu'on a choisi).
On compte le nombre d'apparitions de chacun des nombres, la moyenne théorique est connue (nombre total divisé par 16 ou 32).
On calcule l'écart-type et l'écart probable ep = 2/3 écart type.
On détermine 10 classes :
Nombre d'écarts inférieurs à -4 ep
Nombre d'écarts compris entre -4 ep et -3 ep
...
Nombre d'écarts compris entre 3 ep et 4 ep
Nombre d'écarts supérieurs à 4ep.
On peut reporter ça sur un graphique, on observe une courbe de Gauss. La répartition suivant les classes est (dans l'ordre) 0.35% 2% 7% 16% 25%, à droite et à gauche.
Si vous n'obtenez pas ça, c'est qu'il y a une faute de calcul.
Il est clair qu'il vaut mieux avoir un assez grand nombre de tirages.
Nota, j'ai utilisé un tirage pile ou face plutôt qu'un tirage avec n issues pour éviter toute discussion stérile à propos du générateur utilisé.

Concernant les décimales de pi (par exemple). On sait qu'on peut calculer ces décimales par un développement en série. Chaque terme suivant s'ajoute ai nombre obtenu à l'étape précédente. Ces termes sont de la forme 1/n!.
On calcule en base 10, donc les chiffres obtenue vont de 0 à 9. Ce sont des caractères qui n'ont aucun rapport logique entre eux : leur apparition dépend donc du hasard. Si on calculait en base 16, on aurait le même logique (ou absence de systématisme) et chaque caractère aurait 1 chance sur 16 d'apparaitre.
J'ai eu l'occasion de faire ce contrôle sur un très grand nombre que j'ai trouvé par hasard, d'abord en base 10, puis en base 100, naturellement, c'est vérifié.

Bonne soirée.

[leon1789]

Bonsoir

Par exemple une expérience dont une sortie scalaire suit la loi est uniforme sur [0,1] aura une répartition normale, c'est à dire celle d'une loi gaussienne? Intéressant...

Ben oui, cela ne fait aucun doute. Naturellement, il s'agit de la répartition des écarts à la moyenne dont parle le TCL.

Ben oui... Sauf qu' Amanuensis parle d'une expérience aléatoire à laquelle le TCL ne s'applique pas ! Le TCL ne s'applique pas à une variable (uniforme par exemple, cf Amanuensis), mais à des sommes de variables suivant une même loi (avec quelques hypothèses supplémentaires sur la loi).

[Juzo]

Bonjour, merci pour les détails Dlzlogic !

J'ai appliqué le TCL sur les 800 premières décimales de Pi pour voir la gaussienne de mes propres yeux.
Ci-dessous le résultat pour n = 12 (sommes de 12 termes) et pour N = 792. J'ai pris n = 12 comme exemple car ce serait la valeur à partir de laquelle la loi normale est une bonne approximation.



Je sais, 800 décimales c'est pas beaucoup mais j'ai fait ce que je pouvais !
J'ai comparé l'écart-type à celui obtenu si on avait fait le TCL sur une variable de loi uniforme discrète. L'écart entre les deux écart-types est de 1,65 % environ.
J'ai aussi calculé le pourcentage des différentes classes M - 3 sigma, M - 2 sigma ... si quelqu'un a un commentaire à faire sur ces valeurs !

J'ai fait la même étude pour n = 5, 10, 15, 20 ... Quand la valeur de n est trop grande le pourcentage d'erreur par rapport à la loi uniforme augmente, sûrement car on a pas assez de sommes pour faire une courbe correcte ...

Petit détail amusant : à la 756ème décimale il y a 6 fois de suite le chiffre 9, ce qui a une chance sur 100 000 de se produire quand on fait 6 tirages successifs je ne m'abuse !

Quelques questions maintenant :

- Et maintenant ? L'obtention d'une gaussienne ne montre pas qu'on a des variables aléatoires indépendantes de même loi non ?
C'est quand même un bon moyen de pouvoir éliminer une telle hypothèse dans d'autres situations... Les deux nombres proposés par gg0, 0,12345... et la suite de fibbonacci n'y résistent pas.

Je vous mets un extrait trouvé sur le site pi314 pour donner matière à réflexion.

"Les Chudnovsky écrivaient en 1991 que les décimales de Pi apparaissaient plus aléatoire que ce qui serait généré à la main, mais peut-être tout de même pas assez aléatoires !
La loi du logarithme itéré de Chung décrite sur la page consacrée aux phénomènes aléatoires a suggéré à ces mêmes Chudnovsky de considérer une marche aléatoire de séquences de décimales (rappelons qu'avec le théorème de Donsker, une somme de marches aléatoires
converge en gros vers un mouvement Brownien). A partir de là, on peut construire des objets fractales à partir des décimales de Pi, et pourquoi pas mesurer leurs dimension fractale ! Ben oui, ça c'est une bonne idée !
La dimension fractale d'un processus classique comme le mouvement Brownien est 1.5.
Vanouplines, de l'université de Belgique, a montré que la dimension de Pi est elle aussi très proche de 1.5"

- Finalement, les trois définitions d'une suite aléatoire (voir lien wiki message #1) peuvent-elles s'appliquer à une suite finie ou pas ?

Je ne voulais pas me concentrer sur le nombre Pi, mais apparemment on ne peut pas aller beaucoup plus loin sur les suite aléatoires.

[invite9dc7b526]

rappelons qu'avec le théorème de Donsker, une somme de marches aléatoires
converge en gros vers un mouvement Brownien

c'est pas ça le théorème de Donsker.

[Juzo]

Théorème (Donsker, 1951) Modifier
La suite converge en loi vers un mouvement brownien standard B quand n tend vers l'infini.

Ici B est vu comme un élément aléatoire de (C([0 ; 1]),B) .

Wikipedia encore

[Amanuensis]

- Et maintenant ? L'obtention d'une gaussienne ne montre pas qu'on a des variables aléatoires indépendantes de même loi non ?

Prenez la suite des décimales de pi, vous les groupez par deux ; soit (n, m) une paire, si n est impair et m pair, vous remplacez par (m, n).

Par exemple 14 15 92 65 35 89 79 devient 41152965358979

Et vous passez le "test" sur la suite obtenue.

(La recette doit pouvoir être "améliorée"...)

[invite51d17075]

bonjour juzo,
je regardais ton graphique et j'ai une question stupide.
pourquoi : moyenne attendue 56 et pas 54 ?

[invite9dc7b526]

L'obtention d'une gaussienne ne montre pas qu'on a des variables aléatoires indépendantes de même loi non ?

Un théorème de Cramér dit que si Z=X+Y est normale, X et Y indépendantes, alors X et Y sont normales. L'indépendance est cruciale.

[Juzo]

bonjour juzo,
je regardais ton graphique et j'ai une question stupide.
pourquoi : moyenne attendue 56 et pas 54 ?

Oups c'est une erreur de ma part ! J'ai finalisé ce graphique un peu tard et j'ai pas pensé à vérifier ce calcul...

Le pourcentage "d'erreur" sur la moyenne est donc 0.3367... ce qui est bien mieux

[Juzo]

Un théorème de Cramér dit que si Z=X+Y est normale, X et Y indépendantes, alors X et Y sont normales. L'indépendance est cruciale.

Je crois que dans ce cas Z converge vers une loi normale mais n'est pas une loi normale, donc ce théorème ne peut pas s'appliquer non ?

[Juzo]

Prenez la suite des décimales de pi, vous les groupez par deux ; soit (n, m) une paire, si n est impair et m pair, vous remplacez par (m, n).

Par exemple 14 15 92 65 35 89 79 devient 41152965358979

Et vous passez le "test" sur la suite obtenue.

je veux bien le faire, mais si je garde n = 12 ça ne va rien changer. Ce test doit permettre de vérifier quoi ?

[Amanuensis]

je veux bien le faire, mais si je garde n = 12 ça ne va rien changer. Ce test doit permettre de vérifier quoi ?

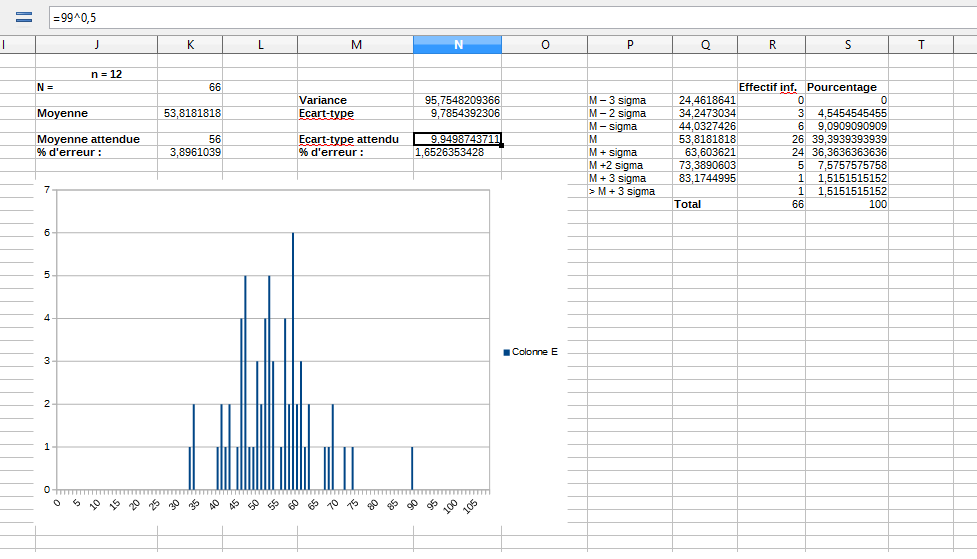
De répondre à la question "L'obtention d'une gaussienne ne montre pas qu'on a des variables aléatoires indépendantes de même loi non ?"

[Juzo]

Ah oui, c'était plutôt une question réthorique, je me doutais de la réponse ; ) Bonne idée en tout cas... Je suis content de ne pas m'être tapé le boulot pour rien

[Amanuensis]

On est d'accord que la suite obtenue n'est ni indépendante, ni uniformément distribuée?