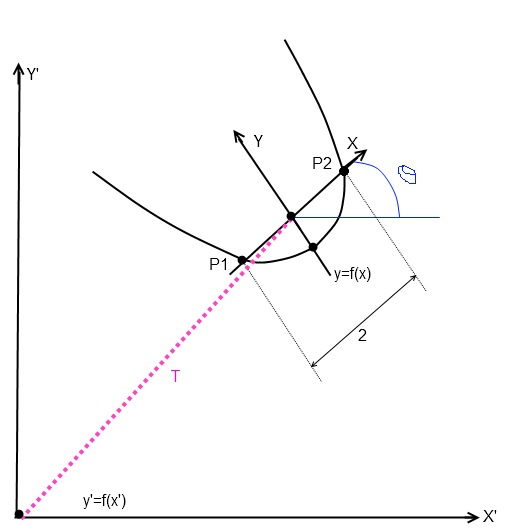
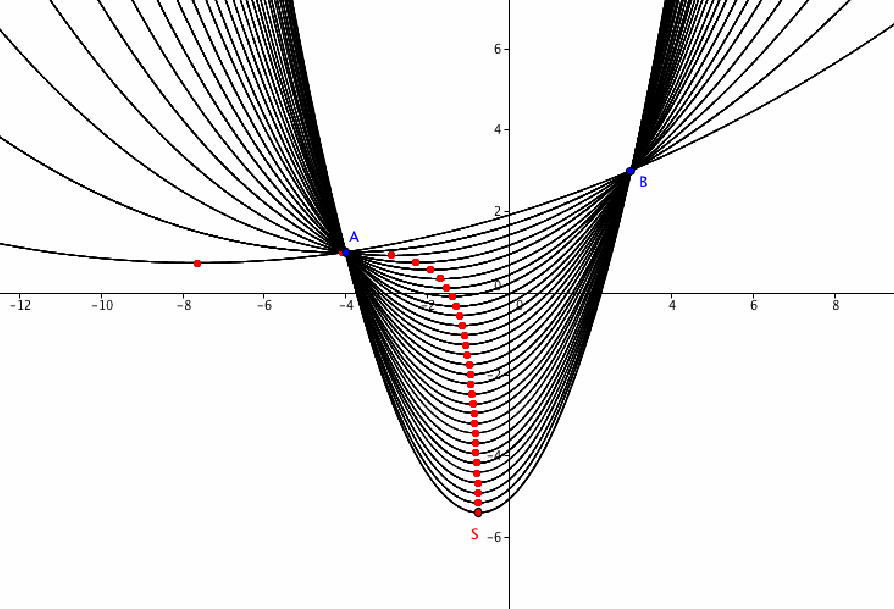
Lieu des sommets d'une parabole passant par deux points donnés
Discussions similaires
-
Par invitebbd6c0f9 dans le forum Mathématiques du collège et du lycée
Réponses: 9
Dernier message: 19/05/2013, 15h28
-
Par invite702b3a82 dans le forum Mathématiques du supérieur
Réponses: 15
Dernier message: 24/04/2012, 09h01
-
Par invite8ff91a85 dans le forum Mathématiques du supérieur
Réponses: 2
Dernier message: 19/01/2010, 18h08
-
Par invitea7a3849b dans le forum Mathématiques du collège et du lycée
Réponses: 23
Dernier message: 17/11/2007, 19h08
-
Par invite72b92f5e dans le forum Mathématiques du supérieur
Réponses: 1
Dernier message: 11/08/2006, 18h34
et
qui ne dépende pas de a, je galère un peu